In the previous problem, initially the insect is at the edge and the disc is rotating with angular speed ω0 in clockwise direction. Now the insect starts walking along the rim with speed v relative to the disc also in clockwise direction. Find new angular speed of platfrom.

By the conservation of angular momentum about O
12MR2ω0=12MR2ω'+m(v+Rω)R'
[speed of insect with respect to the ground (v+rω')]
12MR2ω0−mvR=(12MR2+mR2)ω'
ω'=Mω0−2mvRM+2m
Topper's Solved these Questions
Similar Questions
Suppose the platform with the kid in the previous problemis rotting in anticlockwise directioin at an angular speed ω. The kid starts walking along the rim with a speed v relative to the platform also in the anticlockwise direction. Find the new angular speed of the platform.
View SolutionIn previous problem, if initially the platform with the child is rotating with an angular speed ω1. If child start walking along its periphery in opposite direction with speed u relative to platform, what will be the new angular speed ofthe platform.
View Solution
Knowledge Check
- Question 1 - Select One
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
AKinetic energyBPotential energyCLinear momentumDAngular momentum - Question 2 - Select One
A disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
A(1/2)MR2ωBMR2ωC(3/2)MR2ωD2MR2ω - Question 3 - Select One
A disc is freely rotating with an angular speed ω on a smooth horizontal plane. If it is hooked at a rigid pace P and rotates without bouncing about a point on its circumference. Its angular speed after the impact will be equal to.
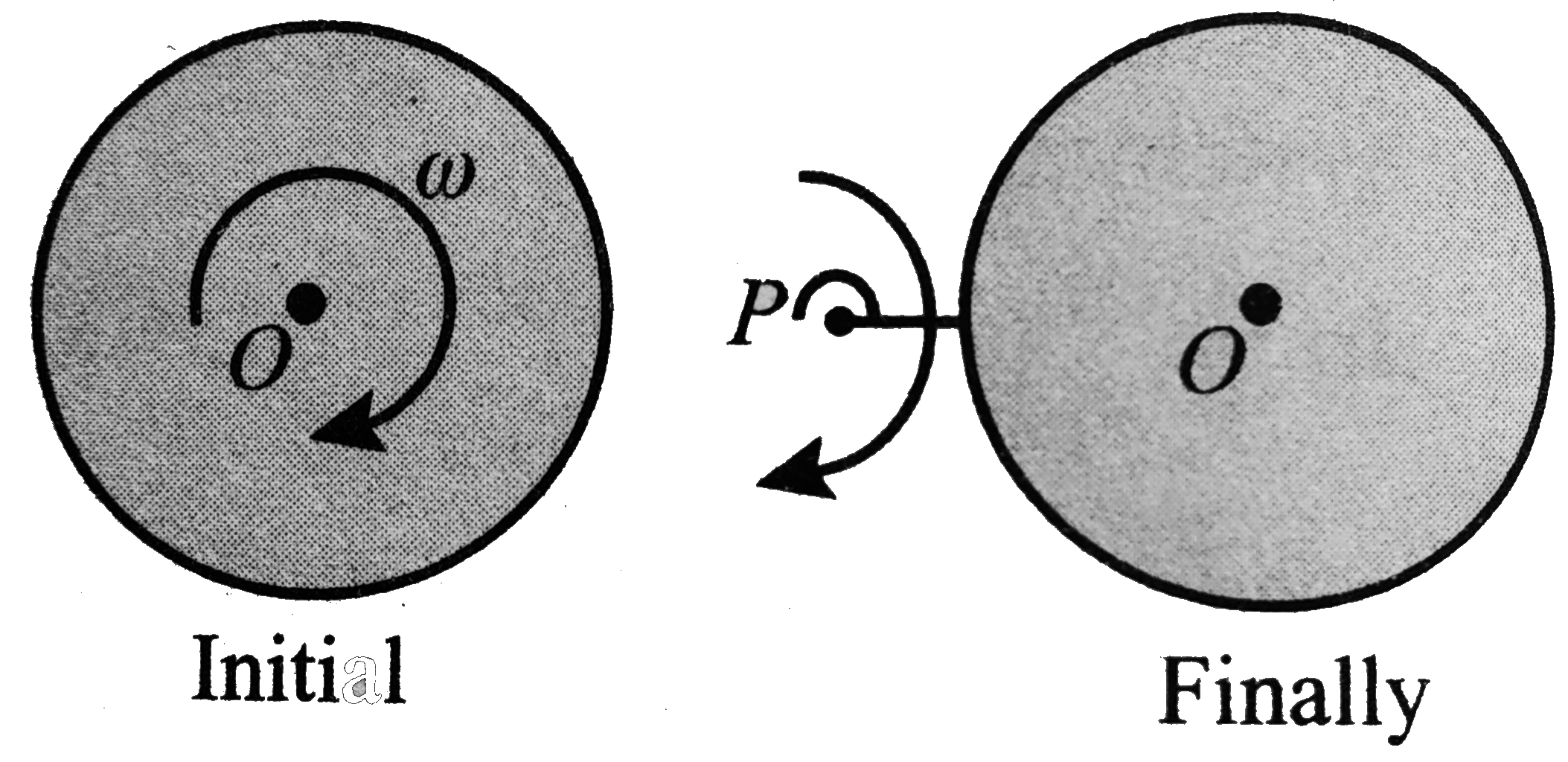 A2ω3Bω3Cω2Dnone of the above
A2ω3Bω3Cω2Dnone of the above
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then
 View Solution
View SolutionA heavy circular disc of mass M is revolving in a horizontal plane with angular speed ω0 about its center which is fixed. An insect of mass m walks from the center to the edge and then files away. Find the final angular speed of disc.
View SolutionA disc of moment of inertia I1 is rotating freely with angular speed ω1 when another non-rotating disc of moment of inertia I2 is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
View SolutionA horizontal disc of radius R and mas 20 M is pivoted to rotate freely about a vertical axis through its centre. A small insect A of mass M and another small insect B of mass mM4 are initially at diametrically opposite points on the periphery of the disc. The whole system is imparted an angular speed ω0 Insect A walks along the diameter with constant velocity v relative to the disc unit it reaches B which remains at rest on the disc. A then eats B and returns to its starting point along the original path with same speed v relative to the disc.
(a) Find the angular speed of the disc when A reaches the centre after eating B.
(b) Plot approximately, the variation of angular speed of the disc with time for the entire journey of the insect A.View SolutionSuppose the platform of the previous problem is brought to rest with the ball in tehhad of the kid standin on the rim. The kid throuws the ball horizontaly to his friend in a direction tangentiasl to the rim with a speed v as seen by his friend. Find the angular velocity wilth which the platform will start rotating.
View Solution

