A thin uniform rod of mass M and length L is lying on a smooth horizontal floor. It is struck by a force F normally at one end. The contact lasts for a very small time t0. Find the distance traveled by the rod in the time in which it is turned by π/2.
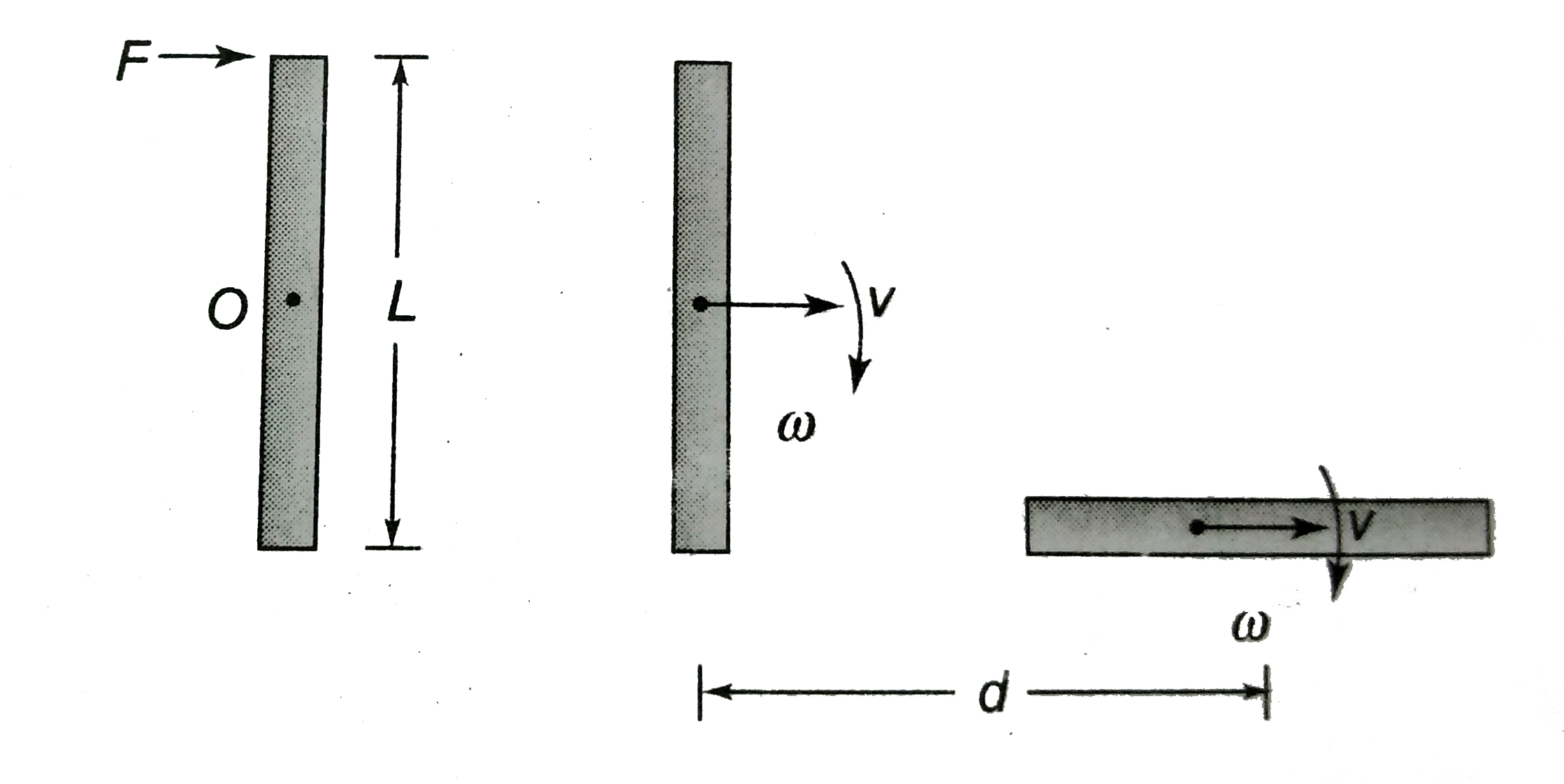
Linear impulse Ft0=Δp=M(v−0)=Mv (i)
Angular impulse FL2t0=ΔL=I0(ω−0)=ML212ω (ii)
Dividing (ii) by (i), we get
L2=L2ω12v⇒ω=6vL
Angular motion, θ=ωt (iii)
Linear motion, d=vt (iv)
Dividing (iv) by (iii), we have
dθ=vω=L6⇒d=L6θ=L6×π2=πL12
Topper's Solved these Questions
Similar Questions
A uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View Solution
Knowledge Check
A rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
AmglBmgl/2Cmgl4D2mglA uniform smooth rod (mass m and length l) placed on a smooth horizontal floor is it by a particle (mass m) moving on the floor, at a distance l4 from one end elastically (e=1). The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
A2πlBcannot be determinedCπlDnone of the aboveA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A(2πmlpB(2π)(pmlCπml12pDπpml
A uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionA uniform rod of length L lies on a smooth horizontal table. A particle moving on the table strikes the rod perpendicularly at an end and stops. Find the distance travelled by the centre of the rod by the time it turns through a right angle. Show that if the mass of the rod is four times that of the particle, the collision is elastic
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface. An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View Solution
