( $a$ ) A rigid body of radius of gyration $k$ and radius $R$ rolls without slipping down a plane inclined at an angle $θ$ with the horizontal. Calculate its acceleration and the frictional force acting on it.
( $b$ ) If the body be in the form of a disc and $θ = 30^{\circ}$ , what will be the acceleration and the frictional force acting on it.

Video Solution

Text Solution

Verified by Experts

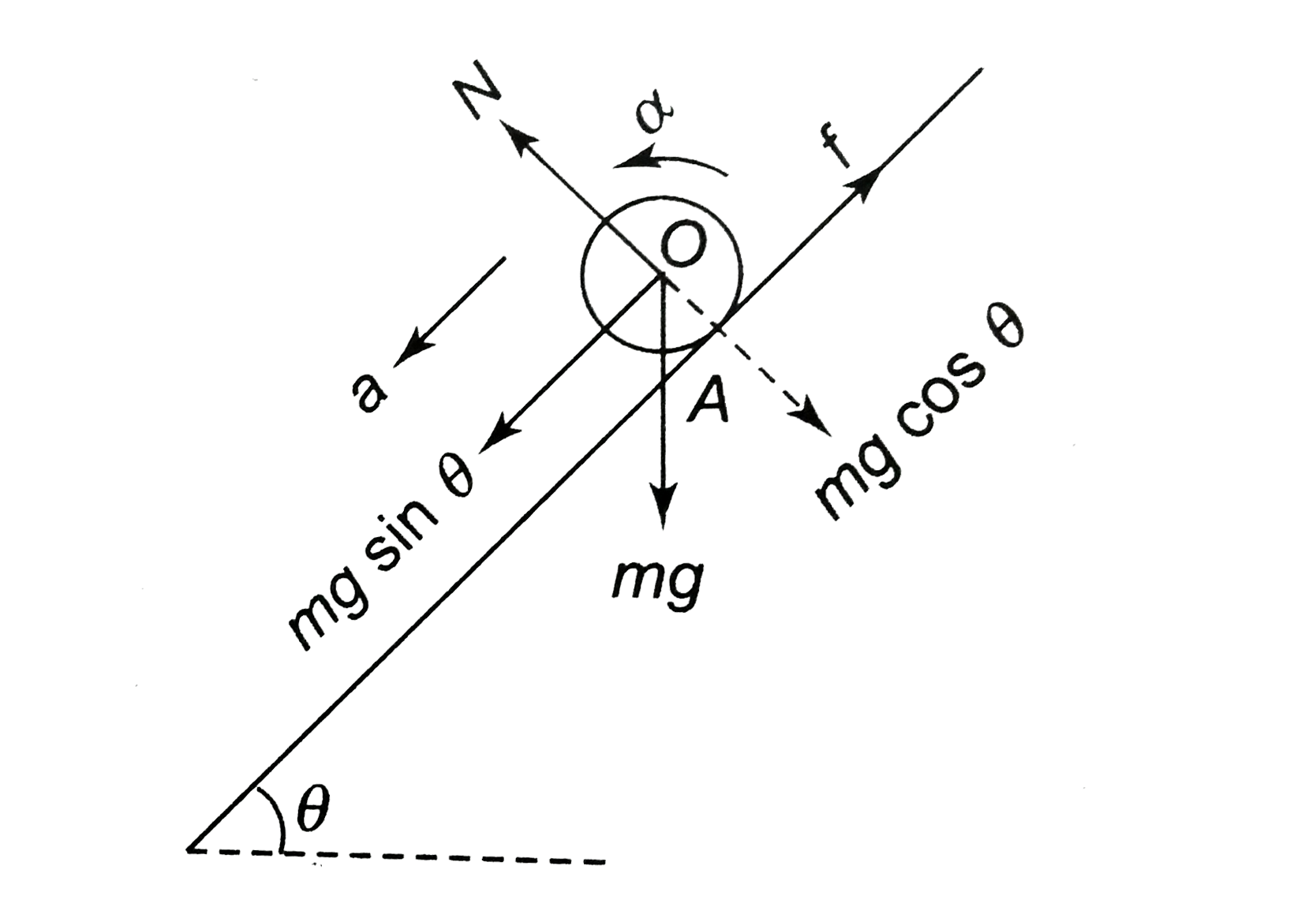
( $a$ ) Due to component $m g sin θ$ , linear velocity is increasing, for pure rolling ( $v_{c . m .} = R ω$ , at anytime), hence angular velocity should increase, for this friction should act upward to provide angular acceleration. Also at the point of contact $A$ , relative acceleration should be zero. Since inclined plane is at rest, hence acceleration of sphere along the plane at $A$ should be zero, i.e.
$a_{A} = a - R α = 0 \Rightarrow a = R α$ ( $i$ )
Linear motion: $m g sin θ - f = m a$ ( $i i$ )
Rotational motion: $τ_{0} = f R = I_{0} α = m k^{2} α$ ( $i i i$ )
$f R = m k^{2} \frac{a}{R} \Rightarrow f = m a \frac{K^{2}}{R^{2}}$ in ( $i i$ )
$m g sin θ - m a \frac{k^{2}}{R^{2}} = m a$
$a (1 + \frac{k^{2}}{R^{2}}) = g sin θ$
$a = \frac{g sin θ}{1 + \frac{k^{2}}{R^{2}}}$ , $f = \frac{m g sin θ}{1 + \frac{R^{2}}{k^{2}}}$
( $b$ ) For disc, $\frac{k^{2}}{R^{2}} = \frac{1}{2}$
$a = \frac{g {sin 30}^{\circ}}{1 + \frac{1}{2}} = \frac{g}{3}$
$f = \frac{g {sin 30}^{\circ}}{1 + 2} = \frac{m g}{6}$

Updated on:21/07/2023