A block of base 10cm×10cm and height 15cm is kept on an inclined plane. The coefficient of friction between them is √3. The inclination θ of this inclined plane from the horizontal plane is gradually increased from 0∘ Then
At θ=30∘, the block will start sliding down the plane
The block will remian at rest on the plane up to certain θ and then it will topple
At θ=60∘, the block will start sliding down the plane and continue to do so at higher angles
At θ=60∘, the block will start sliding down the plane and on further increasing θ, it will topple at certain θ
Condition for sliding:

mgsinθ=f=μmgcosθ
tanθ=μ⇒θ=tan−1(μ)=tan−1(√3)
θ=60∘
Condition for toppling:

Torque about C
N×5=f×152
mgcosθ×5=mgsinθ×152
tanθ=23
θ for toppling<θ for sliding
Topper's Solved these Questions
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
View SolutionA block with a square base measuring axa and height h, is placed on an inclined place. The coefficient of friction is m. The angle of inclination (θ) of the plane is gradually increased. The block will.
View Solution
Knowledge Check
A block of base 10cm×10cm and height 15cm is kept on an inclined plane. The corfficient of friction between them is √3. The inclination θ of this inclined plane from the horizontal plane is gradually increased from 0∘. Then
Aat θ=30∘, the block will starts sliding down the planeBthe block will remain at rest on the plane up to certain θ and then it will toppleCat θ=60∘, the block will start sliding down the plane and continue to do so at higher angles.Dat θ=60∘, the block will start sliding down the plane and on further increasing θ, it will topple at certain θ.A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
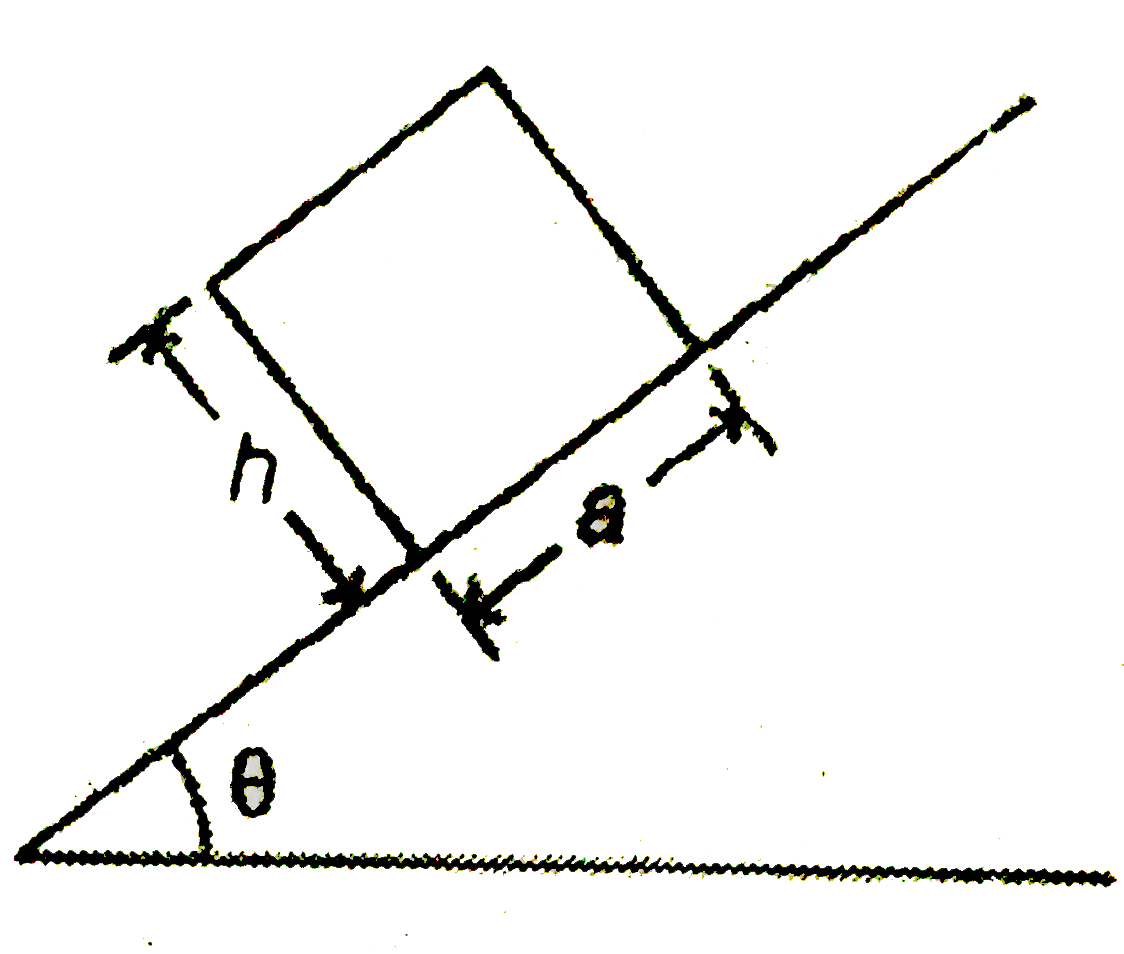 Atopple before sliding if μ>ahBtopple before sliding if μ<ahCslide before toppling if μ>ahDslide before toppling if μ>ah
Atopple before sliding if μ>ahBtopple before sliding if μ<ahCslide before toppling if μ>ahDslide before toppling if μ>ah
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionAn ice cube is kept on an inclined plane of angle 30∘. The coefficient to kinetic friction between the block and incline plane is 1/√3. What is the acceleration of the block ?
View Solution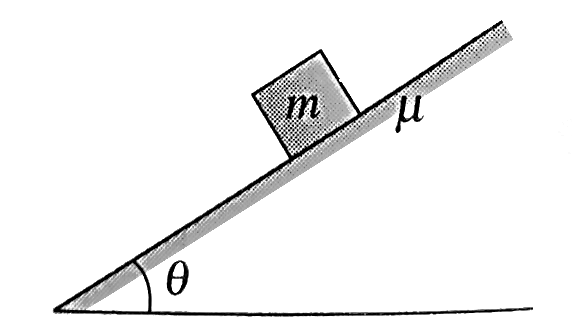 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:
View Solution
