A particle executing simple harmonic motion has angular frequence 6.28s−1 and amplityude 10 cm. Find a the time period, b the maximum speed c. the maximum acceleration d. the speed when thedisplacement is 6 cm from the mean position e. the speed t t=16s assuming that the motion starts from rest t t=0.
ω=6.28=2πrad/s,A=10cm
(a) T=2πω=2π2π=1s
(b) vmax=Aω=10×2π=20πcm/s
(c) amax=Aω2=10×(2π)2=40π2cm/s2
(d) v=ω√A2−x2
=2π√(10)2−(6)2=16πcm/s
(e) Let x=Asin(ωt+ϕ)
v=Aωcos(ωt+ϕ)
At t=0, v=0
cos(ωt+ϕ)=0
cosϕ=cosπ2⇒ϕ=π/2
v=Aωcos(ωt+π/2)=−Aωsinωt
At t=0, x=Asin(ω×0+π/2)=A

At t=16s
v=−Aωsin(ω×1/6)=−10×2πsin(2π/6)
=−10√3πcm/s
At t=1/6s,x=Asin(2π×1/6+π/2)
=Acosπ/3=A/2=5cm
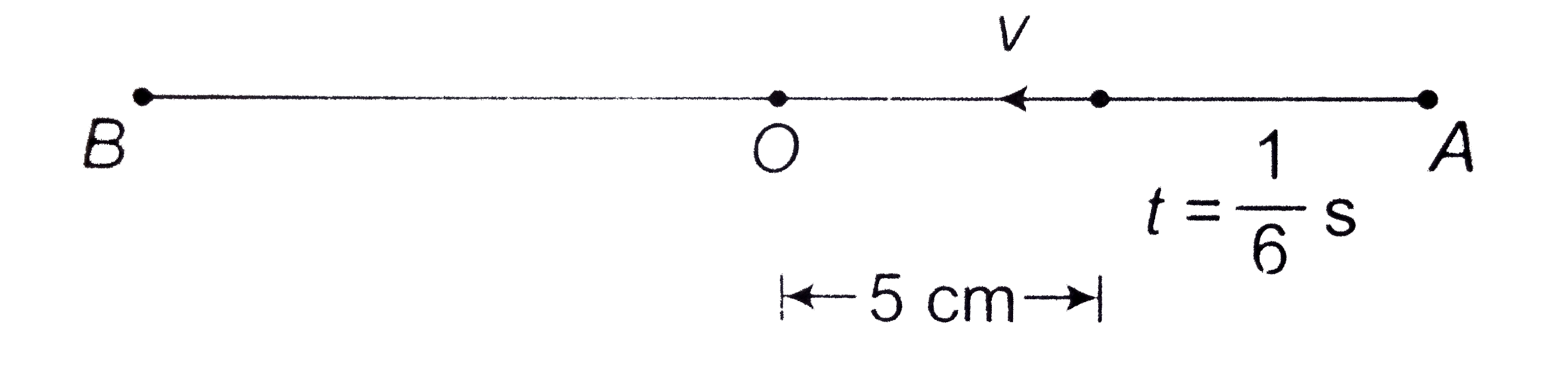
Topper's Solved these Questions
Similar Questions
A particle executing simple harmonic motion has angular frequency 6.28s−1 and amplitude 10cm. Find (a) the time period, (b) the maximum speed, (c) the maximum acceleration, (d) the speed when the displacement is 6cm from the mean position, (e) the speed at t=1/6s assuming that the motion starts from rest at t=0.
View SolutionA particle executing S.H.M. has angular frequency 6.28s−1 and amplitude 10 cm find (a) the time period (b) the maximum speed ( c ) the maximum acceleration (d) the speed when the displacement is 6 cm from the mean postiton ( e ) the speed at t=1/6s assuming that the motion starts from rest at t=0
View Solution
Knowledge Check
- Question 1 - Select One
A particle executes simple harmonic motion with a of period of 6 s and amplitude of 3 cm. Its maximum speed (in cm/s) i
AπB2πC3πD4π - Question 2 - Select One
A particle executing simple harmonic motion has an amplitude of 6 cm. Its acceleration at a distance of 2 cm from the mean position is 8cm/s2. The maximum speed of the particle is
A8cm/sB12 cm/sC16 cm/sD24 cm/s - Question 3 - Select One
For a particle executing simple harmonic motion, the amplitude is A and time period is T. The maximum speed will be
A4ATB2ATC2π√ATD2πAT
A particle is executing simple harmonic motion with an amplitude of 10 cm and time period of 4s. Calculate its displacement, velocity and acceleration after 1/2 seconds, starting from the mean position.
View SolutionA particle of mass 2 kg executing SHM has amplitude 10 cm and time period 1s. Find (a) the angular frequency (b) the maximum speed (c ) the maxmum acceleration (d) the maximum restoring force ( e) the speed when the displacement from the mean position is 8 cm (f) the speed after 112s the particle was at the extreme position (g) the time taken by the particle to go directly from its mean position to half the amplitude (h) the time taken by the particle to go directly from its extreme position to half the amplitude.
View SolutionA particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
View SolutionA particle executing simple harmonic motion has an amplitude of 6 cm . Its acceleration at a distance of 2 cm from the mean position is 8cms2 The maximum speed of the particle is
View SolutionA particle starts simple harmonic motion from the mean position. If It's amplitude is A and time period T, then at a certain instant, its speed is half of its maximum speed at this instant, the displacement is
View Solution

