A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 2∘ and time period 2s. Find a the radius of the circular wire. b. the speed of the particle farthest away from the point of suspension as it goes though its mean position c. the aceleration of this particle as ilt goes through its mean position and extreme position. Take g=π2sms−2
(a) 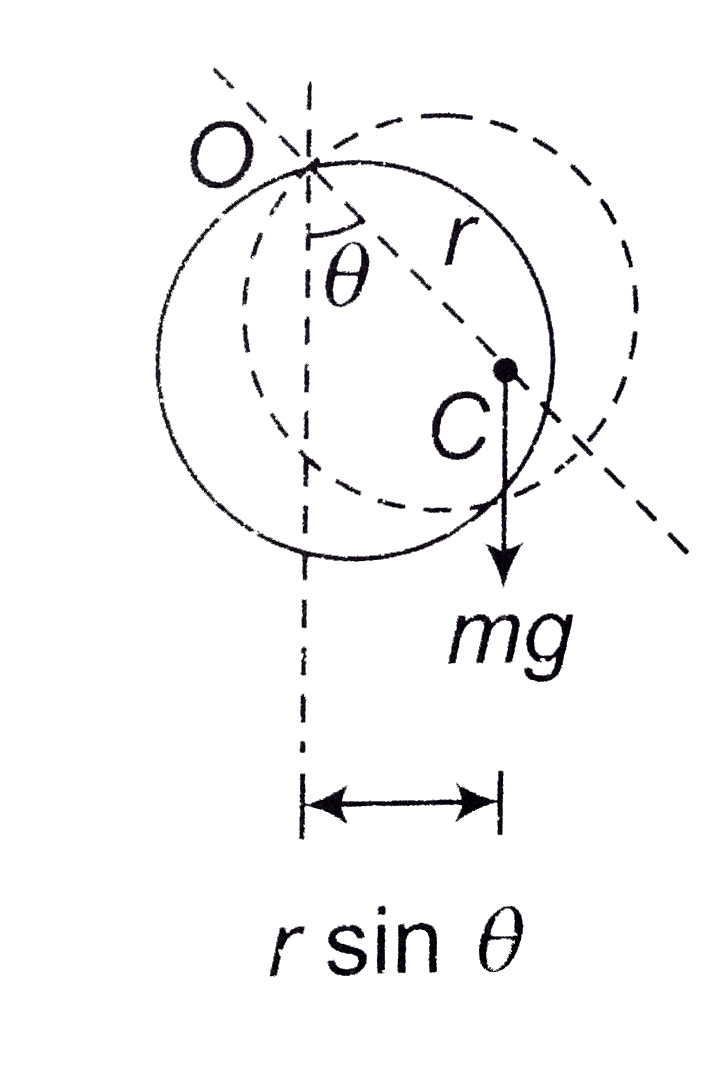
τ=−mgrsinθ
I=mr2+mr2=2mr2
τ=−mgrθ (∵sinθ=θ)
Iα=−mgrθ
α=−mgrIθ=−ω2θ
T=2π√Imgr=2π√2mr2mgr=2π√2rg
T2=4π2⋅2rg
r=gT28π2=10×(2)28×10=0.5m=50cm
(b) 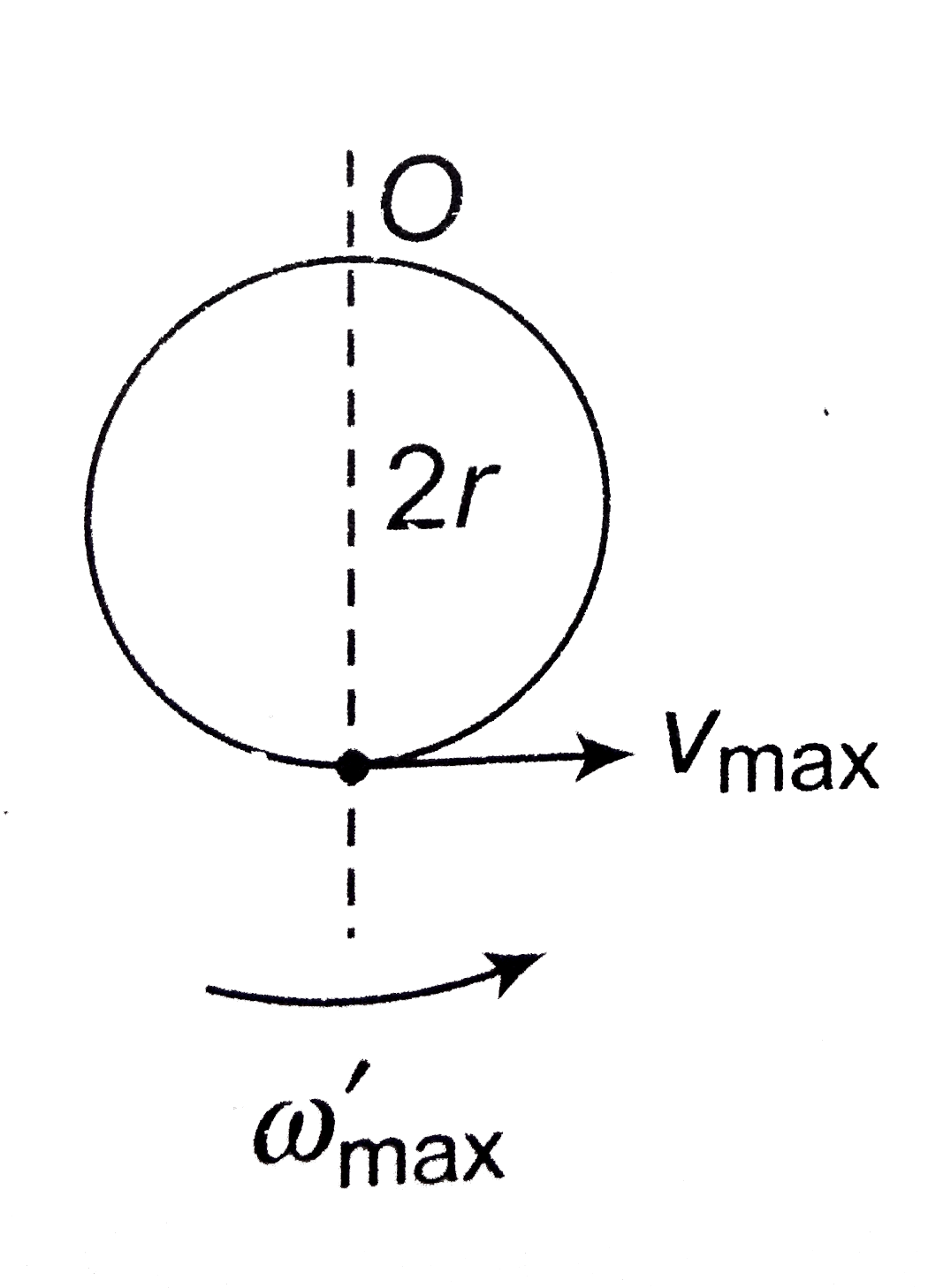
θ0=2∘=2π180=π90rad
ω=2πT=2π2=π
ω′max=θ0ω=π90×π=π290=1090=19rad/s
vmax=2rω′max=2×0.5×19=19m/s
(c) ac=v2max2r=(1/9)22×0.5=181m/s2, towards O
(d) In extreme position, ac=0
a1=2rα=2rω2θ0
=2×0.5×(π)2×π90=π9m/s2
Topper's Solved these Questions
Similar Questions
A particle executes SHM of amplitude 20cm and time period 2s. What is the minimum time required for the particle to move between two points 10cm on either side of the mean position?
View SolutionA particle is executing SHM of amplitude 10 cm. Its time period of oscillation is π seconds. The velocity of the particle when it is 2 cm from extreme position is
View Solution
Knowledge Check
- Question 1 - Select One
A particle performs a S.H.M. of amplitude 10 cm and period 12s. What is the speed of the particle 3s, after pas"sin"g through its mean position ?
A5 cm/sB10 cm/sCZeroD7.5 cm/s - Question 2 - Select One
A particle doing simple harmoonic motion amplitude =4cm time peiod =12sec The ratio between time taken by it in going from its mean position to 2cm and from 2cm to exterme position is
A1B1/3C1/4D1/2 - Question 3 - Select One
A particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
AAB4AC8ADzero
A particle executes SHM with a time period of 4 s . Find the time taken by the particle to go from its mean position to half of its amplitude . Assume motion of particle to start from mean position.
View SolutionThe equation of a simple harmonic oscillator with amplitude 5 cm and period 2 sec is if particle is starting from the mean positions is–
View SolutionA particle executes S.H.M with time period 12 s. The time taken by the particle to go directly from its mean position to half its amplitude.
View SolutionA particle starts SHM from the mean position. Its amplitude is A and time period is T. At the time when its speed is half of the maximum speed, its displacement y is
View SolutionA particle executes SHM with time period 8 s. Initially, it is at its mean position. The ratio of distance travelled by it in the 1st second to that in the 2nd second is
View Solution

