(a) A uniform disc of radius 5⋅0cm and mass 200g is fixed at its centre to a metal wire, the other end of which is fixed with a clamp. The hanging disc is rotated about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s, find the torsional constant of the wire.
(b) In the previous part, another disc is placed over the first one and the time period of the system become 0.65. Find the M.I. of the second disc about the wire.
(a) 
M.I. of disc, I=12mr2=12×0.2×(5×10−2)2
=25×10−5kgm2
T=0.20s
Time period
T=2π√Ik, k: torsional constant
k=4π2IT2=4×(3.14)2×25×10−5(0.2)2
=0.25kg−m2/s2
(b) T=2π√Ik
T′=2π√I+I′k
(ii), (i)
T′T=√I+I′I
0.60.2=(1+I′I)12
1+I′I=9
I′=8I=8×25×10−5
=2×10−3kgm2
Topper's Solved these Questions
Similar Questions
A uniform of radius 5.0cm and mass 200g is fixed at its centre to a metal wire , the other end of which is fixed to a celling. The hanging disc is rotate about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s , find the torsional constant of the wire.
 View Solution
View SolutionThe moment of inertia of the disc used in a torsional pendulum about the suspension wire is 0.2kg−m2. It oscillates with a period of 2s. Asnother disc is placed over the first one and time period of the system becomes 2.5s. Find the moment of inertia of the second disc about the wire.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A circular disc fixed at its centre to a metal wire and the other end of the wire is clamped. The disc is rotated about the wire as axis and is released. The disc about this axis makes simple harmonic oscillations with a frequency of 12Hz. If moment of inertia of the disc about this axis is 0.1 kg −m2, the torsional constant of the wire is
A0.99 kg m2s−2B0.45 kg m2s−2C09.9 kg m2s−2D0.49 kg m2s−2
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View SolutionA circular disc of mass 12 kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and then released, so that the time period of torsional oscillation is 2 s. If the radius of the disc is 10 cm, then calculate the torsional spring constant of the wire.
View SolutionA circular disc of mass 10kg is suspended by a wire attahced to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15cm. Determing the torsional spring constant of the wire. (Torsional spring constant α is definied by the relation J=−αθ, where J is the restoring coubple and θ the angle of twist.
View Solution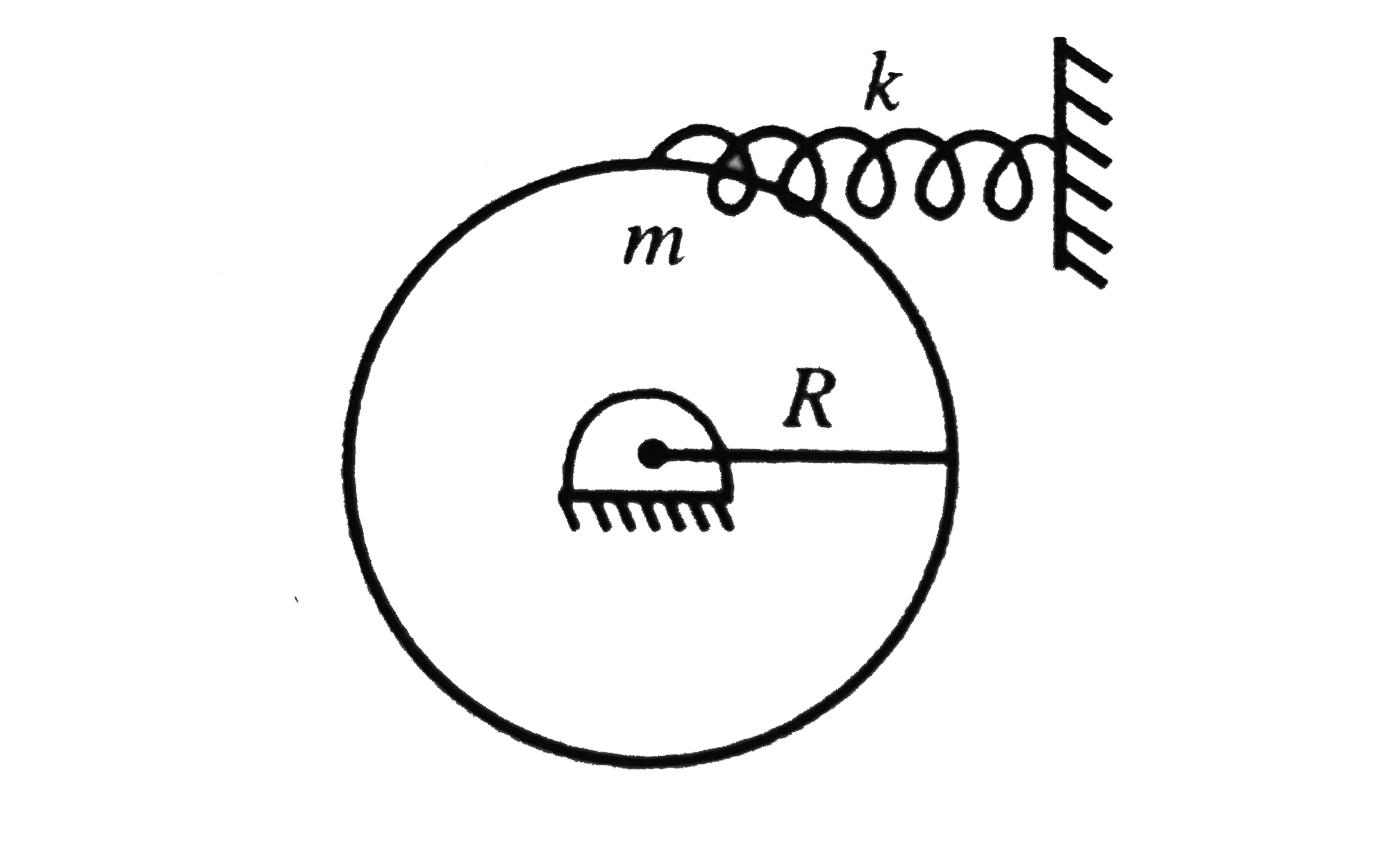
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)View SolutionA disc of radius 2m and mass M is rotating with 200 rpm. Find torque required to stop disc in 10 secs.
View SolutionTwo small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
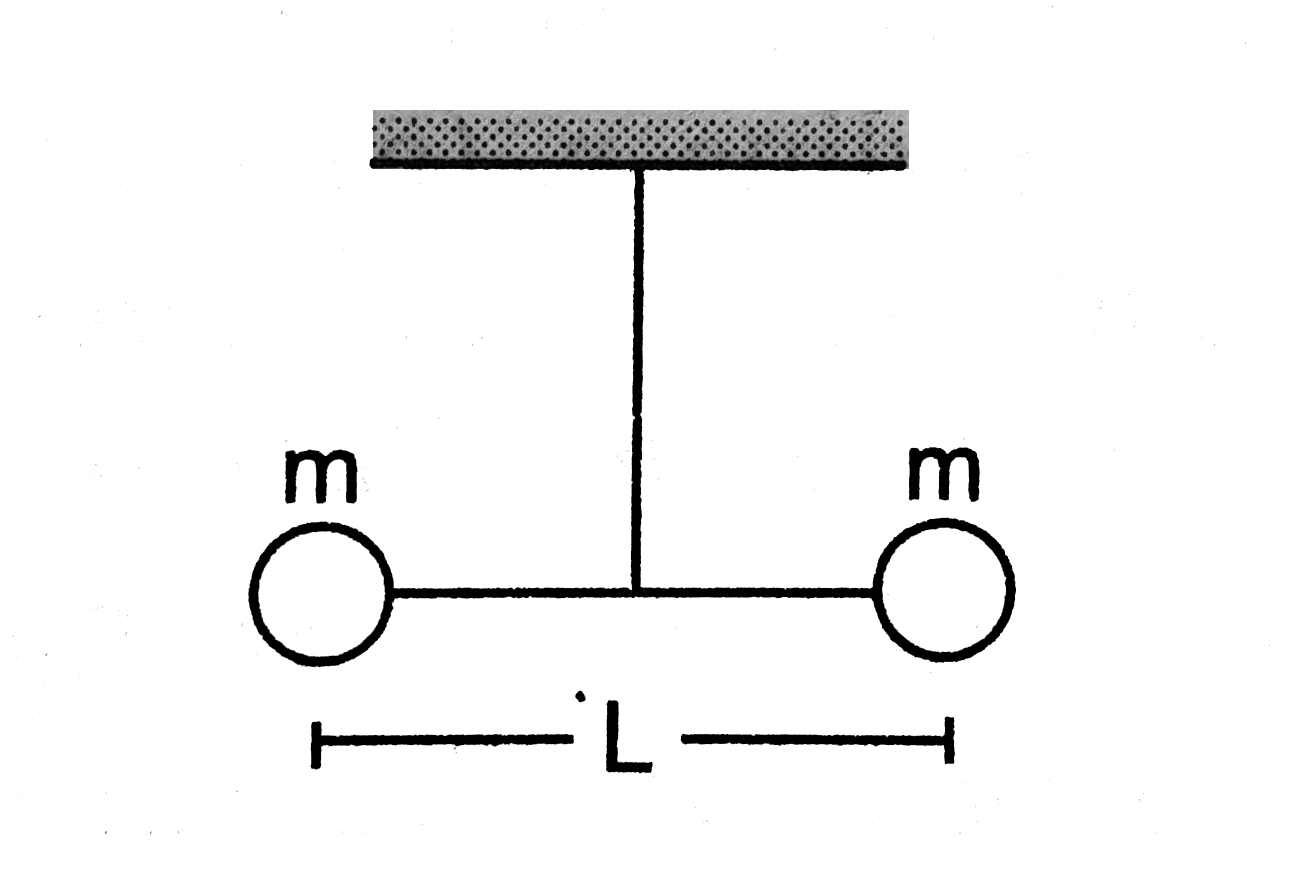 View Solution
View SolutionA string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
View Solution

