A uniform plate of mass M stays horizontally symmetrically on two wheels rotating in opposite directions. The separation between the wheels is L. the friction coefficient between each and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

Let the plate be displaced towards right by x and released.

N1+N2=mg
Taking torque about A
N2L=mg(L2+x), N2=mg(12+xL)
N1=mg(12−xL)
Restoring force
F=−(f2−f1)=−μ(N2−N1)=−μ2mgxL
a=Fm=−2μgLx=−ω2x
T=2π(L2μg)
Topper's Solved these Questions
Similar Questions
A uniform table of mas M stays horizontally and symmetrically on two wheels rotatig in opposite directions figure. The separsation between the wheels is L. The friction coefficeint between each whee, and the plate is μ. Find the time period of oscilationof the pate if it is slightly displaced along its length and released.
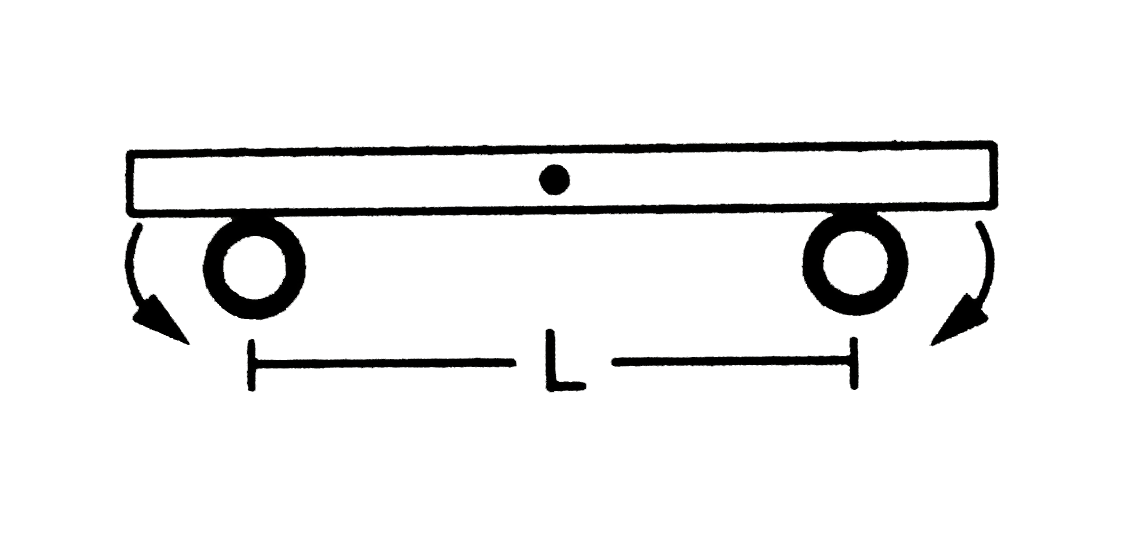
View SolutionA uniform table of mas M stays horizontally and symmetrically on two wheels rotatig in opposite directions figure. The separsation between the wheels is L. The friction coefficeint between each whee, and the plate is μ. Find the time period of oscilationof the pate if it is slightly displaced along its length and released.

View Solution
Knowledge Check
The coin is notating with a plate without sliding If the coefficient of friction between the coin and plane is μ=0.75 the friction between the coin and plate is

If the plate is rotating along and the coin is gently placed on the rotating plate, the frictional force on the coin isAmgB32mgCmg2D34mg
Two wheels which are rotated by some external source with constant angular velocity in opposite directions as shown in figure. A uniform plank of mass M is placed on it symmetrically. The friction co-efficient between each wheel and the plank is μ. find the frequency of oscillations, when plank is slightly displaced along its length and released.

View SolutionTwo wheels which are rotated by some external source with constant angular velocity in opposite directions as shown in figure. A uniform plank of mass M is placed on it symmetrically. The friction co-efficient between each wheel and the plank is μ. find the frequency of oscillations, when plank is slightly displaced along its length and released.

View SolutionA uniform horizontal plank is resting symmetrically in a horizontal position on two cylindrical droms , which are apinning in in opposite direction about their horizontal axes with equal angular velocity . The distance between the axes with equal angular velocity. The distance between the axes is 2L and the coefficient of friction between the plank and cylender is μ . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple horizontal motion. Caculate also the time period of motion.
View SolutionA uniform horizontal plank is resting symmetrically in a horizontal position on two cylindrical droms , which are apinning in in opposite direction about their horizontal axes with equal angular velocity . The distance between the axes with equal angular velocity. The distance between the axes is 2L and the coefficient of friction between the plank and cylender is μ . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple horizontal motion. Caculate also the time period of motion.
View SolutionThe coin is notating with a plate without sliding If the coefficient of friction between the coin and plane is μ=0.75 the friction between the coin and plate is

If the plate is rotating along and the coin is gently placed on the rotating plate, the frictional force on the coin is
View SolutionA uniform rod is placed on two spinning wheels as shown in figure. The axes of the wheels are separated by a distance l=20cm, the coefficient of friction between that in this case the rod performs harmonic oscillations. Find the period of these oscillations.

View SolutionA plank rests symmetrically on two cylinders which are separated by a distance of 2l and rotate with uniform speed in opposite direction. If the plank is displaced a little and then released, show that the motion of the plank is simple harmonic. Calculate the period of oscillations of the peak. The co-efficient of friction between the plank and either cylinder is μ.
View Solution
