(a) A particle is subjected to two simple harmonic motions
$x_{1} = A_{1} sin ω t$ and $x_{2} = A_{2} sin (ω t + π / 3)$ .
Find (i) the displacement at $t = 0$ , (ii) the maximum speed of the particle and (iii) the maximum acceleration of the particle.
(b) A particle is subjected to two simple harmonic motions, one along the x-axis and the other on a line making an angle of $45^{\circ}$ with the x-axis. The two motions are given by
$x y = x_{0} sin ω t$ and $s = s_{0} sin ω t$
Find the amplitude of the resultant motion.

Video Solution

Text Solution

Verified by Experts

(a) $x_{1} = A_{1} sin ω t$ , $x_{2} = A_{2} sin (ω t + π / 3)$
$x = x_{1} + x_{2} = A sin (ω t + ϕ)$

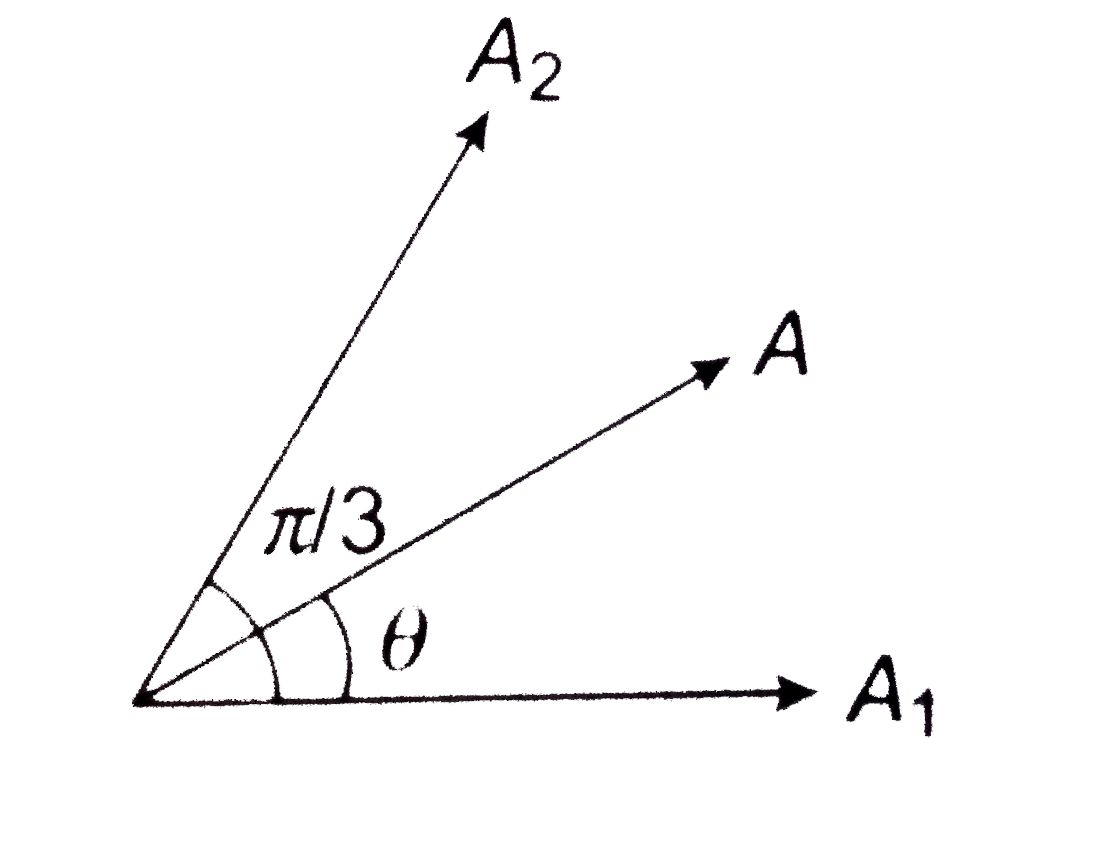
$A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} cos (ϕ = π / 3)}$
$= {(A_{1}^{2} + A_{2}^{2} + A_{1} A_{2})}_{1}^{\frac{1}{2}}$
$tan θ = \frac{A_{2} sin π / 3}{A_{1} + A_{2} \frac{cos π}{3}} = \frac{A_{2} \times \sqrt{3} / 2}{A_{1} + A_{2} \times 1 / 2}$
$= \frac{\sqrt{3} A_{2}}{2 A_{1} + A_{2}}$
(i) $x = A sin (ω t + θ)$
At $t = 0$ , $x = A sin θ$
$= {(A_{1}^{2} + A_{2}^{2} + A_{1} A_{2})}_{1}^{\frac{1}{2}} \frac{{\sqrt{A}}_{2}}{{(4 A_{1}^{2} + A_{2}^{2} + 4 A_{1} A_{2} + 3 A_{2}^{2})}_{1}^{\frac{1}{2}}}$
$= \frac{\sqrt{3} A_{2}}{2}$
OR
$t = 0$ , $x_{1} = A_{1} sin ω t = 0$ ,
$x_{2} = A_{2} sin (ω t + π / 3) = \frac{\sqrt{3} A_{2}}{2}$
$x = x_{1} + x_{2} = \frac{A_{2} \sqrt{3}}{2}$
(ii) $v_{max} = ω A = ω {(A_{1}^{2} + A_{2}^{2} + A_{1} A_{2})}_{1}^{\frac{1}{2}}$
(iii) $a_{max} = ω^{2} A = ω^{2} {(A_{1}^{2} + A_{2}^{2} + A_{1} A_{2})}_{1}^{\frac{1}{2}}$
(b) $x = x_{0} sin ω t$ along x-axis
$s = s_{0} sin ω t$ along $y = x$ line
component of s along coordinate axes
$x^{'} = s_{0} sin ω t {cos 45}^{\circ} = \frac{s_{0}}{\sqrt{2}} ω t$
$y^{'} = s_{0} sin ω t {sin 45}^{\circ} = \frac{s_{0}}{\sqrt{2}} sin ω t$
$X = x + x^{'} = (x_{0} + \frac{s_{0}}{\sqrt{2}}) sin ω t$ , $Y = y^{'} = \frac{s_{0}}{\sqrt{2}} sin ω t$
$r = \sqrt{X^{2} + Y^{2}} = {⎡ ⎣ {(x_{0} + \frac{s_{0}}{\sqrt{2}})}_{0}^{2} + {(\frac{s_{0}}{\sqrt{2}})}^{2} ⎤ ⎦}^{\frac{1}{2}} sin ω t$
Resultant amplitude
$= {⎡ ⎣ {(x_{0} + \frac{s_{0}}{\sqrt{2}})}_{0}^{2} + {(\frac{s_{0}}{\sqrt{2}})}^{2} ⎤ ⎦}^{\frac{1}{2}} = {[x_{0}^{2} + s_{0}^{2} + \sqrt{2} x_{0} s_{0}]}_{0}^{\frac{1}{2}}$

Updated on:21/07/2023