The amplitude and maximum velocity will be respectively X=3sin2t+4cos2tThe amplitude and maximum velocity will be respectively
5,10
3,2
4,2
3,4
The correct Answer is:A
x=3sin2t+4cos2t
=5[35sin2t+45cos2t]
=5[cosαsin2t+sinαcos2t]
x=5sin(2t+α)
v=dxdt=5×2cos(2t+α)
=10cos(2t+α)
Amplitude A=5, vmax=10
Alternatively:
x=3sin2t+4cos2t
=3sin2t+4sin(2t+π2)
x=Asin(2t+α)
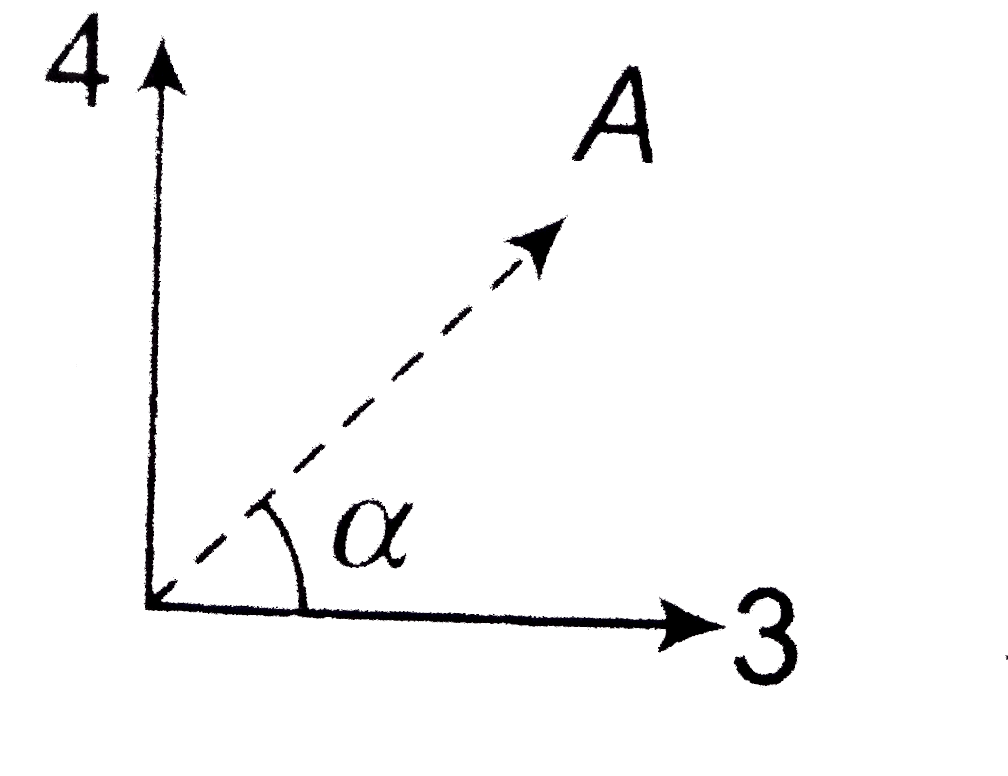
A=√32+42=5
tanα=43
x=5sin(2t+α)
v=dxdt=5×2cos(2t+α)
=10cos(2t+α)
v is maximum when cos(2t+α)=1
vmax=10
Topper's Solved these Questions
Similar Questions
If the maximum and minimum value of sinsinx is a and b respectively and the maximum and minimum value of coscosx is c and d respectively then a2+b2+c2+d2: (A) 1+a2 (B) 2+a2 (C) 3+a2 (D) 4+a2
View SolutionA particle is executing S.H.M. with amplitude 'A' and maximum velocity Vm. The displacement at which its velocity is half of the maximum velocity is
View Solution
Knowledge Check
- Question 1 - Select One
If S=9t−3t3, then maximum velocity is
A0B−9 units / secC9 units/ SecD10 units /sec - Question 2 - Select One
A SHO has amplitude A and time period T. The maximum velocity will be
A4ATB2ATC2π√A/TD2πA/T - Question 3 - Select One
For a particle in SHM the amplitude and maximum velocity are A and V respectively. Then its maximum acceleration is
AV22ABV2ACV2ADVA
In a plane progressive wave given by y=25cos(2πt−πx), the amplitude and frequency are respectively
View SolutionIf S=16+64t−t3, then maximum velocity is
View SolutionThe velocity-time graph of a particle executing SHM is as shown in the figure. The amplitude and maximum acceleration of the particle respectively are
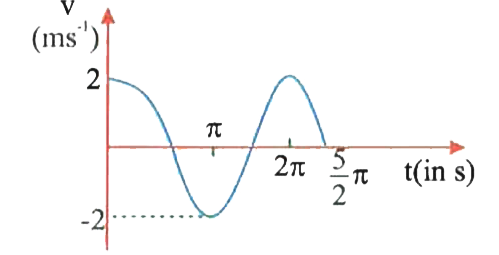 View Solution
View SolutionEquation of displacement of a harmonic oscillator is x=15sin20πt, amplitude and angular velocity are respectively
View SolutionThe displacement ξ in centimetres of a particle is ξ=3sin314t+4cos314t. Amplitude and initial phase are
View Solution

