A man running on a horizontal road at 6km/h finds the rain falling vertically. He doubles his speed and find that the raindrops make an angle 37∘ with the vertical. Find the velocity of rain with respect to the ground.
Let the velocity of rain w.r.t. the ground is u.
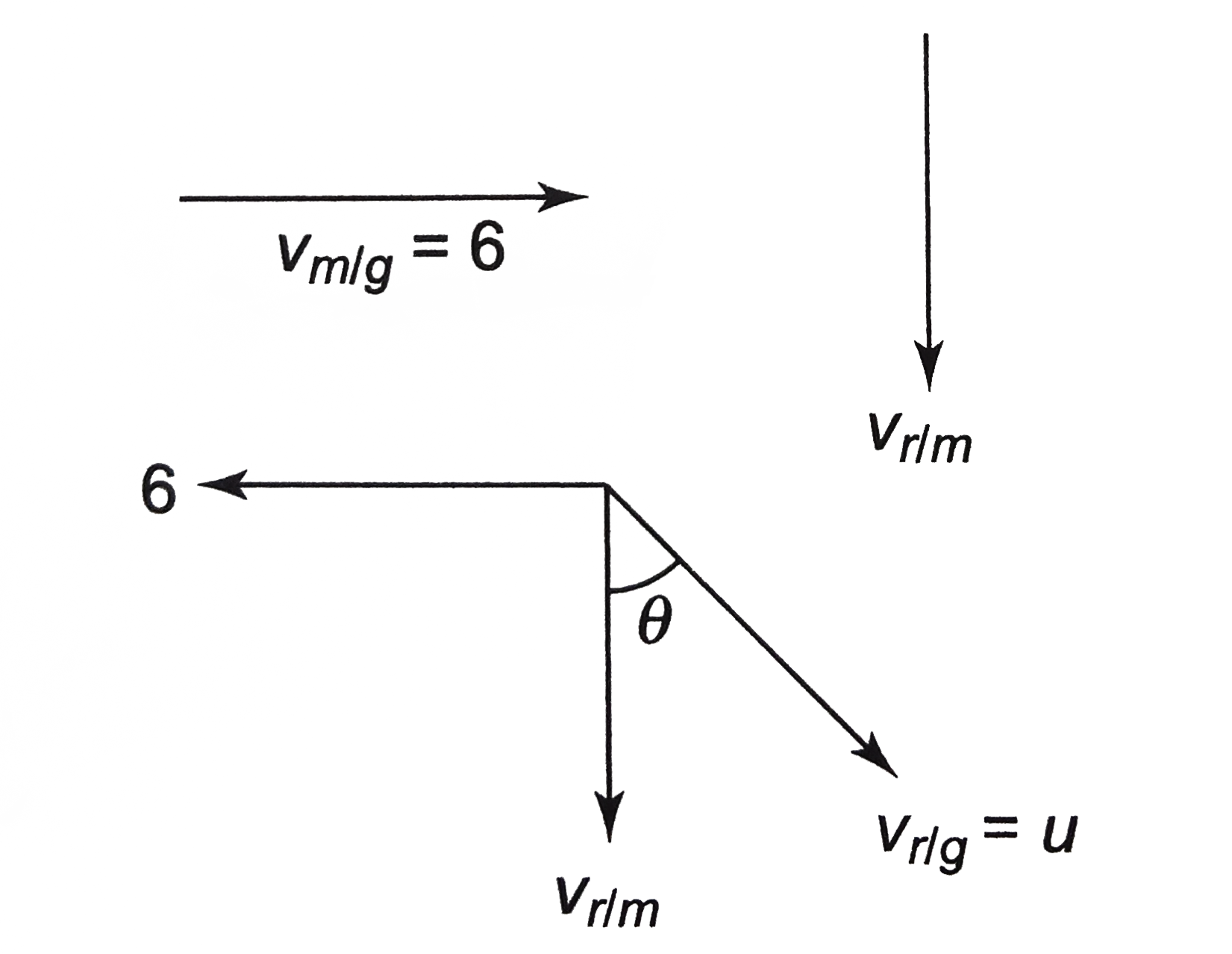
Recall: vr/m is resultant of vr/g and vm/g (in opposite direction).
sinθ−6=0
usinθ=6......(i)
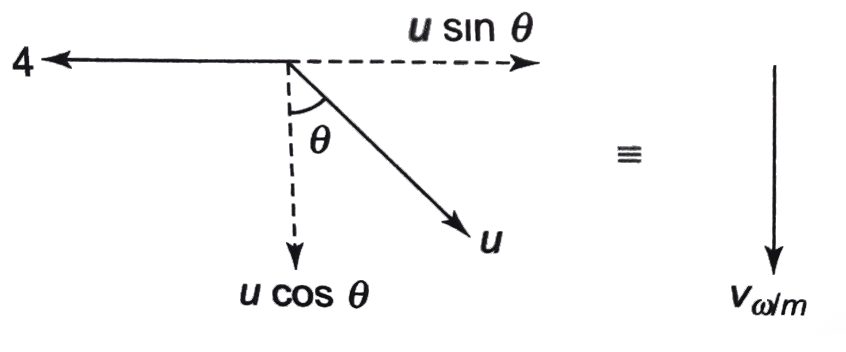
Now the man doubles his speed and vr/m makes 37∘ with vertical, it may be

Recall: Resultant is towards larger vector.

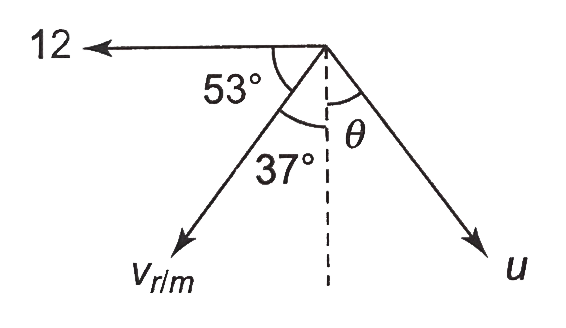
tan53∘=usin(90+θ)12+ucos(90+θ)
43=ucosθ12−usinθ=ucosθ12−6
ucosθ=8..........(ii)
u=√(usinθ)2+(ucosθ)2
=8√(6)2+(8)2=10km/h
tanθ=usinθucosθ=68=34⇒θ=37∘
vr/g=10km/h at an angle 37∘ with vertical direction

Topper's Solved these Questions
Similar Questions
A person walking ,on a horizontal road at 2 km/h finds that the rain is falling vertically . Now the person increasses his speed to 4 km/h and find that rain makes an angle 45∘ with the vertical . Find the velocity of rain with respect to the road.
View SolutionA man running on the horizontal road at 8kmh−1 find the rain appears to be falling vertically. He incresases his speed to 12kmh−1 and find that the drops make angle 302 with the vertical. Fin dthe speed and direction of the rain with respedt to the road.
View Solution
Knowledge Check
A man running on the horizontal road at 8kmh−1 find the rain appears to be falling vertically. He incresases his speed to 12kmh−1 and find that the drops make angle 302 with the vertical. Fin dthe speed and direction of the rain with respedt to the road.
A4√7 km/hB9√7 km/hC12√7 km/hD15√7 km/hA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
Auˆi−utanθˆjBuˆi−ucotθˆjCuˆi+ucotθˆjDutanθˆi−uˆjA man running at a speed of 5 km/h finds that the rain is falling vertically. When the stops running, the finds that the rain is falling at an angle of 60∘ with the horizontal. The velocity of rain with respect to running man is
A5√3 km/hB5√32 km/hC4√35 km/hD5√3 km/h
A man walking with a speed of 3 km/h finds the rain drops falling vertically downwards. When the man increases his speed to 6km/h he find that the rain drops are falling making an angle of 30∘ with the vertical . Find the speed of the rain drops ( in km/h)
View SolutionThe rain is falling vertically downward with velocity 6m/s and a man is moving horizontally with velocity 8m/s. Find the velocity of rain with respect to the man.
View SolutionTo a man walking at 5kmph rain appears to fall vertically, and when he doubles his speed it appears to make an angle of 30∘ with the vertical. Find the actual velocity of the rain. In what direction will rain appear to fall if the man suddenly turns around when his speed is 5 kmph?
View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.
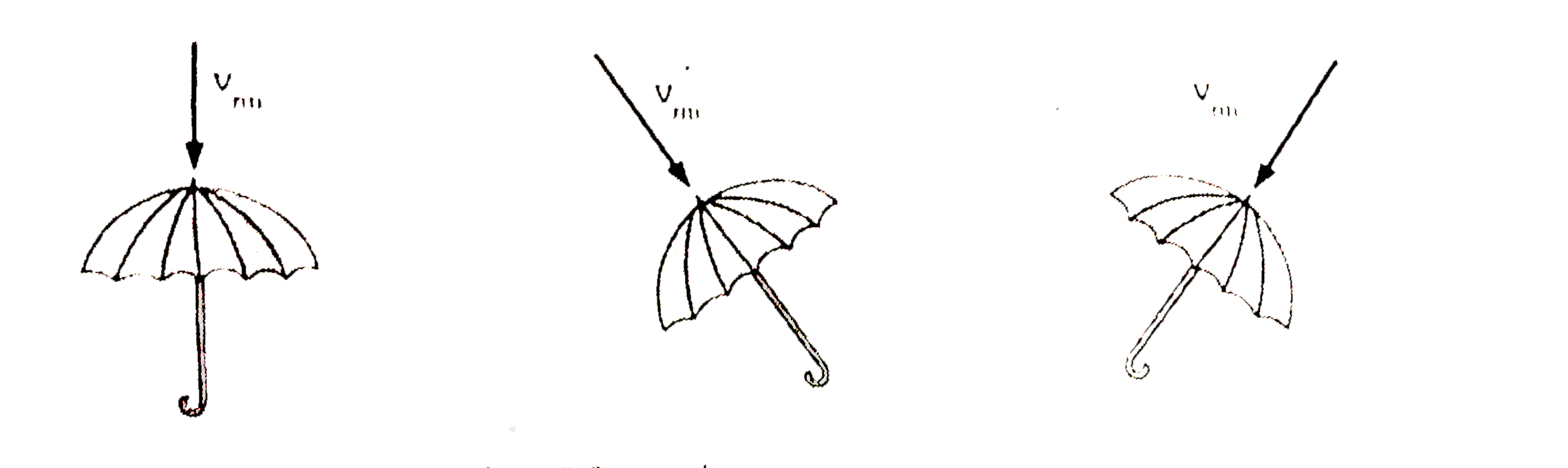
A man walks in rain at 72 cm/m due east and observes the rain falling vertically. When he stops, rain appears to strike his back at 37∘ from the vertical. Find velocity of raindrops relative to the ground.
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View Solution
