In the previous problem, the man wants to cross the river in the minimum time. In which directions, he should move? Find the minimum time to cross the river and his displacement (drift) along the flow.
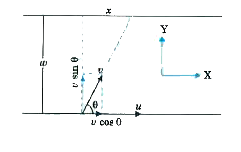
y:d=vcosθt
t=dvcosθ
t will be minimum if cosθ is maximum.
(cosθ)max=1
t will be minimum if cosθ is maximum.
(cosθ)max=1
⇒θ=0∘
To cross the river in the minimum time, the man should swim perpendicular to the river flow.

(vm/g)x=u,(vm/g)y=v
y:d=vt⇒t=tmin=dv
x:x=ut=udv
x: drift along the flow
Topper's Solved these Questions
Similar Questions
A man can row a boat with 4km/h in still water, if he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be holded, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river 4km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction shou ld he heat the boat if he wants to cross the river in shorest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point?View SolutionCrossing River In Minimum Time
View Solution
Knowledge Check
- Question 1 - Select One
For a man who wants to cross the river, with the shortest path AB, find the anglet θ (see figure)
 Asin−1(34)Bsin−1(43)C30∘DGiven situation is not possible
Asin−1(34)Bsin−1(43)C30∘DGiven situation is not possible - Question 2 - Select One
Assertion: To cross the river in minimum time swimmer should swimming in perpendicular direction to the water current.
Reason: In this case river flow helps to cross this river.AIf both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.BIf both Assertion & Reason are True but Reason is not correct explanation of the Assertion.CIf Assertion is Trie but the Reason is False.DIf both Assertion & Reason are false - Question 3 - Select One
A man can swim in still water at 4m/s river is flowing at 2m/s. the angle with downstream at which he should swim to cross the river minimum drift is
A120∘B150∘C30∘D60∘
A river is flowing from the west to the east at 5m/min. A swimmer on the southerm bank can swim at 10 m/min in still water. In what direction should he swim if (i) He wishes to cross the river in minimum time (ii) He wishes to cross te river through shortest route
View SolutionA man can swim in still water with a speed v . River flows at a speed u which is greater than the swimming speed (v) of the man . Explain that the man cannot move perpendicular to the flow . If man swims at an angle θ with the river flow , then find drift along the flow by the time he crosses the river . Also find the minimum value of the drift along the flow x by the time he crosses the river .
 View Solution
View SolutionA river of width 100 m is flowing with a velocity of 1.5 m/s. A man start from one end with rest relative the river. He raws with an acceleration of 2m/s2 relative to the river. If the man want to cross the river in minimum time, by how much distance (in meters) will he be drifted (flown) in the direction of river flow during the crossing.
View SolutionA man wishes to cross a river which is flowing at a certain speed . Man uses a motor boat whose velocity with respect to water is more than speed of flow. Minimum possible time the boat takes to cross the river is t1 , but drift along the length of river is x . When boat takes shortest route to cross the river , then it takes time t2 . Find the velocity of boat with respect to water .
View SolutionA river is 12km wide and flows at the rate of 3 kmph. A man, who can swim in still water at the rate of 5 kmph wishes to reach the other bank of the river. In what direction should he start swimmin to cross the river (a) along the shortest route, (b) in the shortest possible time ? Calculate how much time he will take to cross the river in the two cases.
View Solution

