A balloon starts rising from the surface of the earth with a verticle component of velocity v0. The baloon gathes a horizontal velocity vx=λy, where λ is a constant and y is the height from the surface of earth, due to a horizontaln wind. determine (a) the equation of trajectory and (b) the tangential, normal and total acceleration of the balloon as a function of y.
(a) vy0=v0⇒dydt=v0
∫y0dy=v0∫t0dt⇒y=v0t
vx=λy⇒dxdt=λv0t ….(i)
∫x0dx=λv0∫t0tdt⇒x=λv0t22 ……(ii)
Eliminating t between (i) and (ii), we get
x=λyv02(yv0)2 ⇒x=λy22v0 (parabola, open rightward)
(b) vy=v0⇒ay=dvydt=0
vx=λy=λv0t⇒ax=dvxdt=λv0
Total acceleration a=ax=λv−(0)
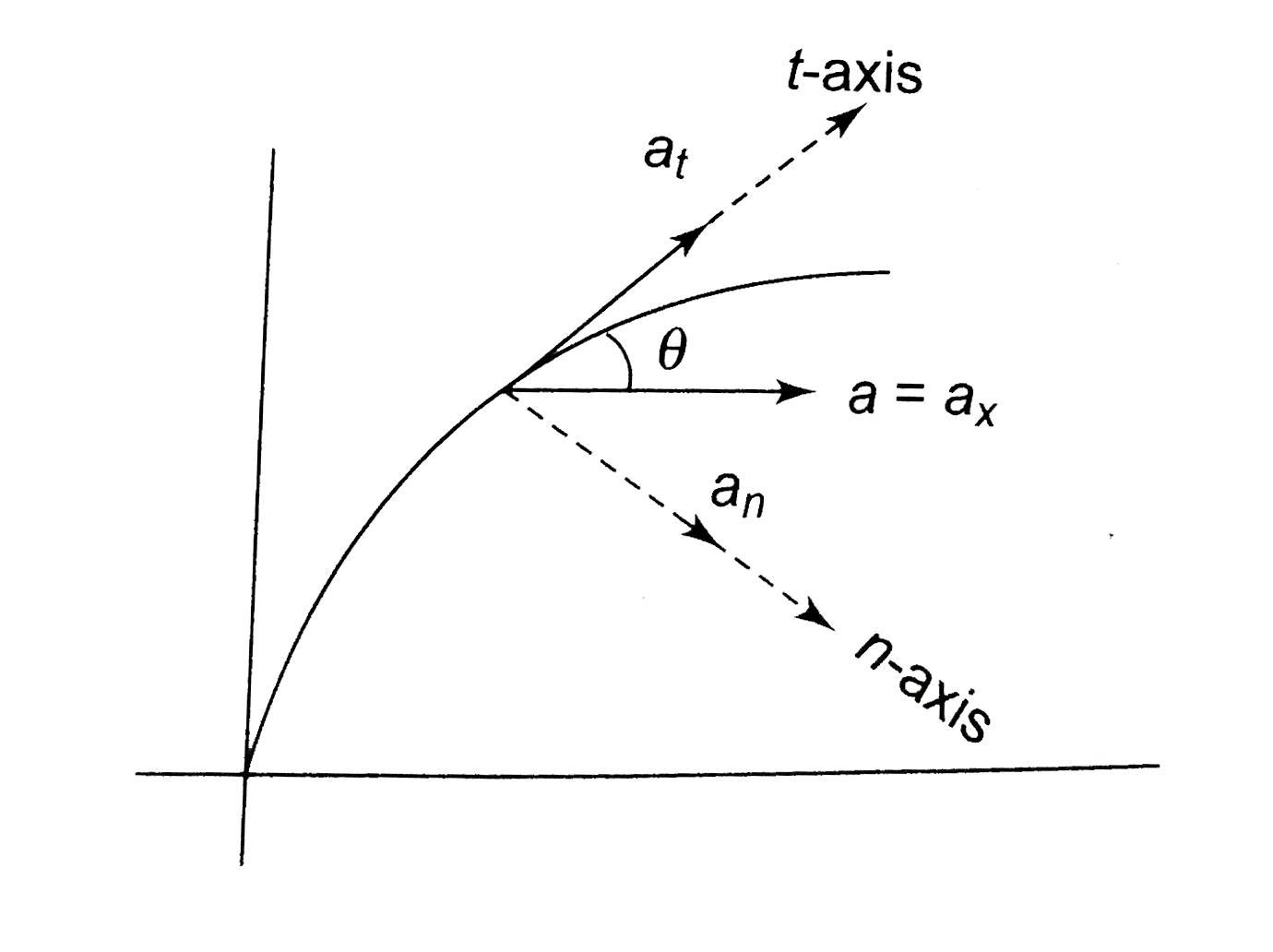
x=λY22V0⇒dx=λ2v02ydy
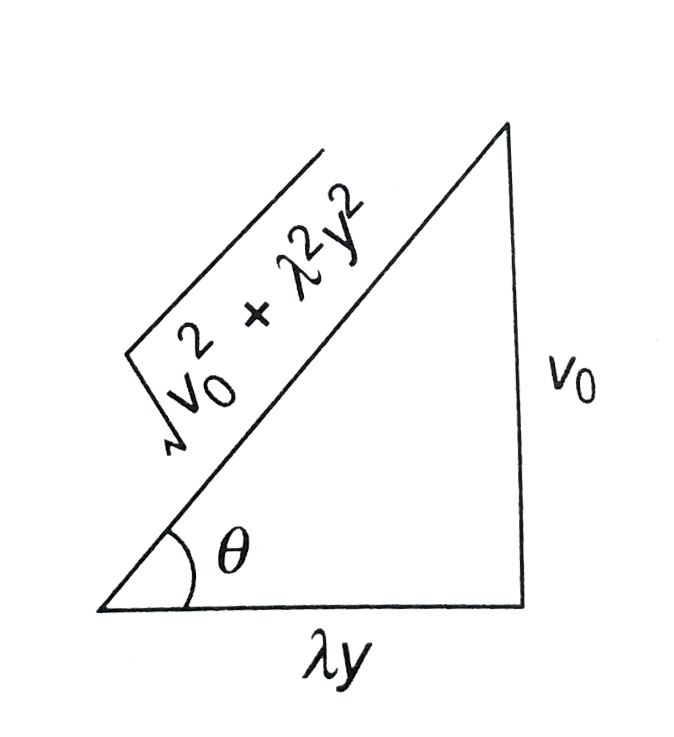
Slope: dydx=tanθ=v0λy
Normal acceleration
an=asinθ=λv0×v0√v20+λ2y2=λv20√v20+λ2y2
Topper's Solved these Questions
Similar Questions
A balloon starts rising from the surface of the earth with vertical component of velocity v0. The balloon gathers a horizontal velocity vx=ay, where a is a constant and y is the height from the surface of the earth, due to a horizontal wind. Determine
(a) the equation of trajectory of the balloon.
(b) the tangential, normal and total acceleration of the balloon as function of y.View SolutionA balloon starts rising from the surface of the Earth. The ascertion rate is constant and equal to v0. Due to the wind the balloon
View Solution
Knowledge Check
- Question 1 - Select One
A ball of mass m is fired vertically upwards from the surface of the earth with velocity nve, where ve is the escape velocity and n<1. Neglecting air resistance, to what height will the ball rise? (Take radius of the earth=R):-
AR/n2BR/(1−n2)CRn2/(1−n2)DRn2 - Question 2 - Select One
The earth is assumed to be a sphere of radius R. A platform is arranged at a height R from the surface of the earth. The escape velocity of a body from this platform is fv, where v is its escape velocity from the surface of the earth. The value of f is
A1/2B√2C1/√2D1/3.
A balloon starts rising from the earth's surface. The ascension rate is constant and equal to v0. Due to the wind. The balloon gathers the horizontal velocity component vx=ky, where k is a constnat and y is the height of ascent. Find how the following quantities depednd on the height of ascent.
(a) the horizontal drift of the balloon x (y)
(b) the total tangential and normal accelrations of the balloon.View SolutionA particle moves in the x-y plane with the velocity ¯v=aˆi−btˆj. At the instant t=a√3/b the magnitude of tangential, normal and total acceleration are _&_.
View SolutionA body is projected up from the surface of the earth with a velocity half the escape velocity at an angle of 30∘ with the horizontal. Neglecting air resistance and earth’s otation, find (a) the maximum height above the earth’s surface to which the body will rise. (b) will the body move around the earth as a satellite?
View SolutionA particle moves in the plane xy with velocity v=ai+bxj, where i and j are the unit vectors of the x and y axes, and a and b are constants. At the initial moment of time the particle was located at the point x=y=0. Find:
(a) the equation of the particle's trajectory y(x),
(b) the curvature radius of trajectory as a function of x.View SolutionA mass is taken to a height R from the surface of earth and then is given horizontal velocity v. The minimum value of v so that mass escapes to infinity is √GMnR. Find the value of n.
View SolutionA body is thrown from the surface of the Earth at an angle α to the horizontal with the initial velocity v0. Assuming the air drag to be negligible, find:
(a) the time of motion,
(b) the maximum height of ascent and the horizontal range, at what value of the angle α they will be equal to each other,
(c) the equation of trajectory y(x), where y and x are displacements of the body along the vertical and the horizontal respectively,
(d) the curvature radii of trajectory at its initial point and at its peak.View Solution

