A ball of mass $m$ is attached to a fixed point by a light inextensible string describe a circle in a verticle plane. The tension in the string has the values $α m g$ and $β m g$ , respectively, when the particle is at the highest and the lowest point in the path. find the relation between $α$ and $β$ .

Video Solution

Text Solution

Verified by Experts

$v^{2} = u^{2} - 2 g \times 2 L = u^{2} - 4 g L$
At the lowest point:
$T_{1} - m g = \frac{μ^{2}}{L}$
$T_{1} - m g = \frac{μ^{2}}{L}$
$β m g = m g + \frac{μ^{2}}{L} \Rightarrow \frac{μ^{2}}{L} = (β - 1) m g$
$T_{2} + m g = \frac{m v^{2}}{L}$
$α m g + m g = \frac{m}{L} (u^{2} - 4 g L)$
$(α + 1) m g = \frac{μ^{2}}{L} - 4 m g$
$(α + 1) m g = \frac{m u^{2}}{L} - 4 m g$
$= (β - 1) m g - 4 m g$
$α + 1 = β - 1 - 4$
$α + 1 = β - 5 \Rightarrow β = α + 6$

|

Updated on:21/07/2023

Class 11 PHYSICS CIRCULAR MOTION

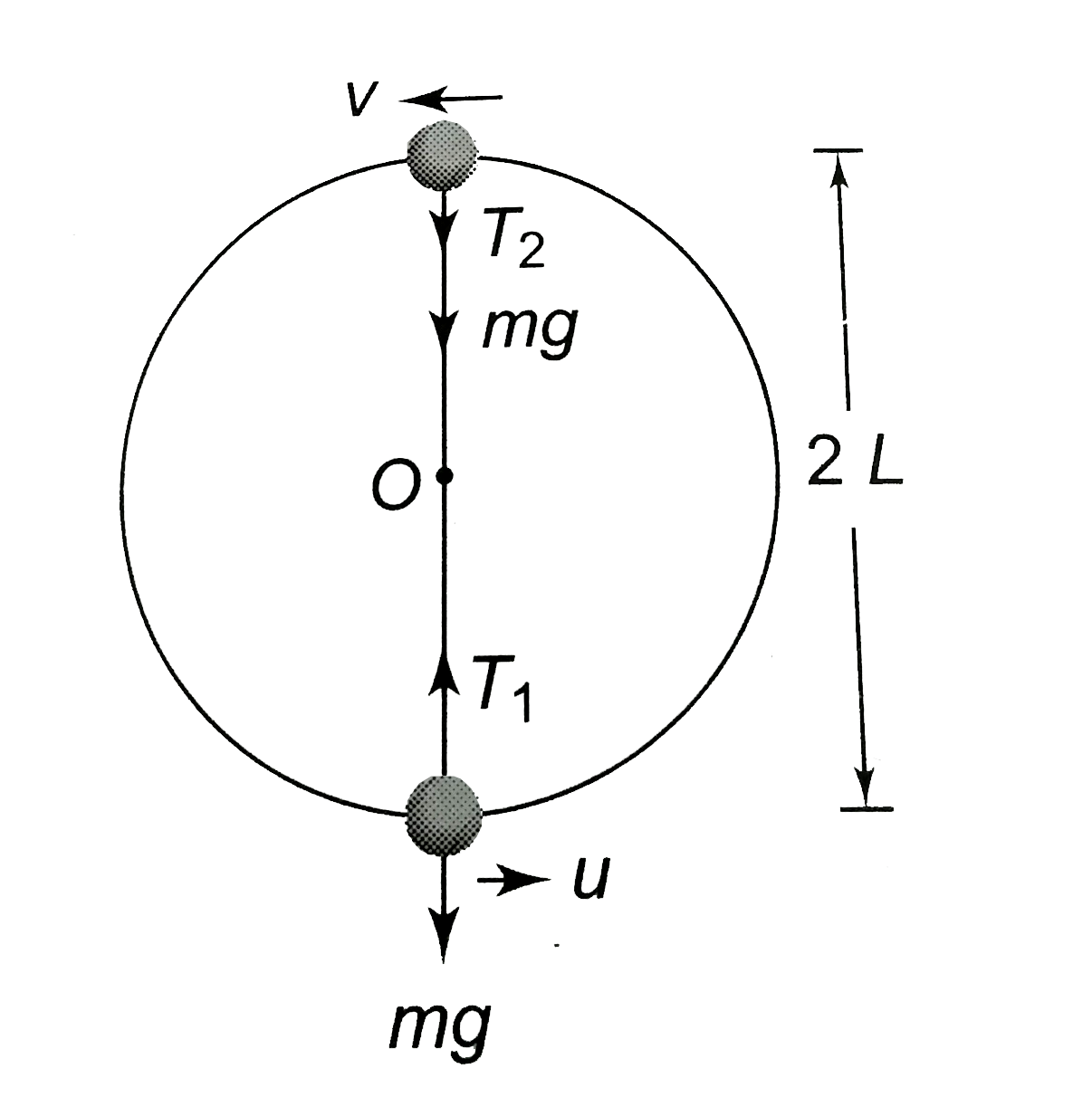
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A heavy particle of weight w, attached to a fixed point by a light inextensible string describes a circle in a vertical plane. The tension in the string has the values nw and mw respectively when the particle is at the highest and lowest points in the path. Then :
A $m + n = 6$
B $\frac{m}{n} = 2$
C $m - n = - 6$
D $n - m = - 6$
Question 2 - Select One
A stone of mass $m$ is tied to a string and is moved in a vertical circle of radius $r$ making $n$ revolution per minute. The total tension in the string when the stone is its lowest point is.
A $m [g + 4 π^{2} r]$
B $m [g + \frac{π^{2} n^{2} r^{2}}{60}]$
C $m [g + \frac{π^{2} n^{2} r}{900}]$
D $m [g + n^{2} r^{2}]$
Question 3 - Select One
A particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is -
A1
Bfinite but large
Czero
DInfinite

CP SINGH-CIRCULAR MOTION-Exercise

Home
Ask Doubt
Profile