A particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
To solve the problem of finding the angle with the vertical at which a particle loses contact with a smooth hemisphere, we can follow these steps:
Step 1: Understand the Geometry
The particle is released from the top of a hemisphere of radius R. When the particle is at an angle θ with the vertical, its height h above the ground can be expressed as:
h=R−Rcosθ=R(1−cosθ)
Step 2: Apply Energy Conservation
The initial potential energy of the particle when it is at the top of the hemisphere is converted into kinetic energy and potential energy when it reaches the angle θ. The initial potential energy is given by:
PEinitial=mgR
The potential energy at height h is:
PEfinal=mg(R(1−cosθ))
The kinetic energy at angle θ is:
KE=12mv2
By conservation of energy, we have:
mgR=mg(R(1−cosθ))+12mv2
Step 3: Simplify the Energy Equation
We can cancel m from all terms (assuming m≠0) and rearranging gives:
gR=gR(1−cosθ)+12v2
This simplifies to:
gRcosθ=12v2
Thus,
v2=2gRcosθ
Step 4: Determine the Forces at Angle θ
At the angle θ, the forces acting on the particle are:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the surface of the hemisphere.
The centripetal force required to keep the particle moving in a circular path is provided by the component of the gravitational force and the normal force:
N+mgcosθ=mv2R
When the particle loses contact, the normal force N becomes zero:
mgcosθ=mv2R
Step 5: Substitute for v2
From the energy conservation equation, we have v2=2gRcosθ. Substituting this into the force equation gives:
mgcosθ=m(2gRcosθ)R
Cancelling m and R (assuming R≠0) gives:
gcosθ=2gcosθ
This leads to:
gcosθ=2gcosθ⟹0=gcosθ
This implies that cosθ must equal u23gR+23.
Step 6: Solve for θ
From the equation derived, we have:
cosθ=u23gR+23
Thus, the angle θ can be expressed as:
θ=cos−1(u23gR+23)
Final Answer
The angle θ at which the particle loses contact with the hemisphere is:
θ=cos−1(u23gR+23)
The particle is released from the top of a hemisphere of radius R. When the particle is at an angle θ with the vertical, its height h above the ground can be expressed as:
h=R−Rcosθ=R(1−cosθ)
The initial potential energy of the particle when it is at the top of the hemisphere is converted into kinetic energy and potential energy when it reaches the angle θ. The initial potential energy is given by:
PEinitial=mgR
The potential energy at height h is:
PEfinal=mg(R(1−cosθ))
The kinetic energy at angle θ is:
KE=12mv2
By conservation of energy, we have:
mgR=mg(R(1−cosθ))+12mv2
We can cancel m from all terms (assuming m≠0) and rearranging gives:
gR=gR(1−cosθ)+12v2
This simplifies to:
gRcosθ=12v2
Thus,
v2=2gRcosθ
At the angle θ, the forces acting on the particle are:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the surface of the hemisphere.
N+mgcosθ=mv2R
When the particle loses contact, the normal force N becomes zero:
mgcosθ=mv2R
From the energy conservation equation, we have v2=2gRcosθ. Substituting this into the force equation gives:
mgcosθ=m(2gRcosθ)R
Cancelling m and R (assuming R≠0) gives:
gcosθ=2gcosθ
This leads to:
gcosθ=2gcosθ⟹0=gcosθ
This implies that cosθ must equal u23gR+23.
From the equation derived, we have:
cosθ=u23gR+23
Thus, the angle θ can be expressed as:
θ=cos−1(u23gR+23)
The angle θ at which the particle loses contact with the hemisphere is:
θ=cos−1(u23gR+23)
Topper's Solved these Questions
Similar Questions
A particle is released from the top of a smooth hemisphere.find the angle rotated by the radius through the particle, when it loses contract with the hemisphere. Also sketch variation of normal contact force with cosθ, where θ is an angle rotated by the radius through the particle.
View SolutionA block of mass as shown is released from rest from top of a fixed smooth hemisphere. Find angle made by this particle with vertical at the instant when it looses contact with hemisphere.
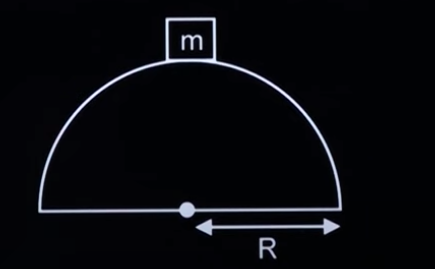 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
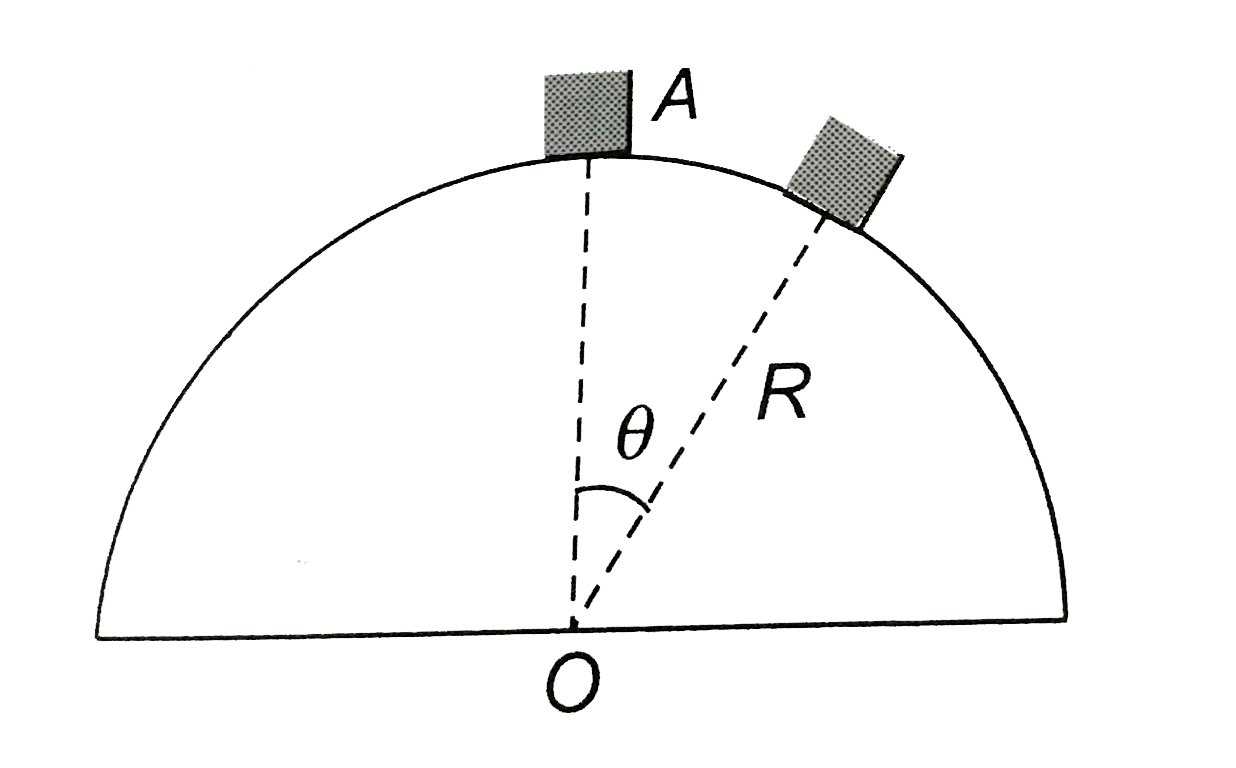 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ) - Question 2 - Select One
A small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?
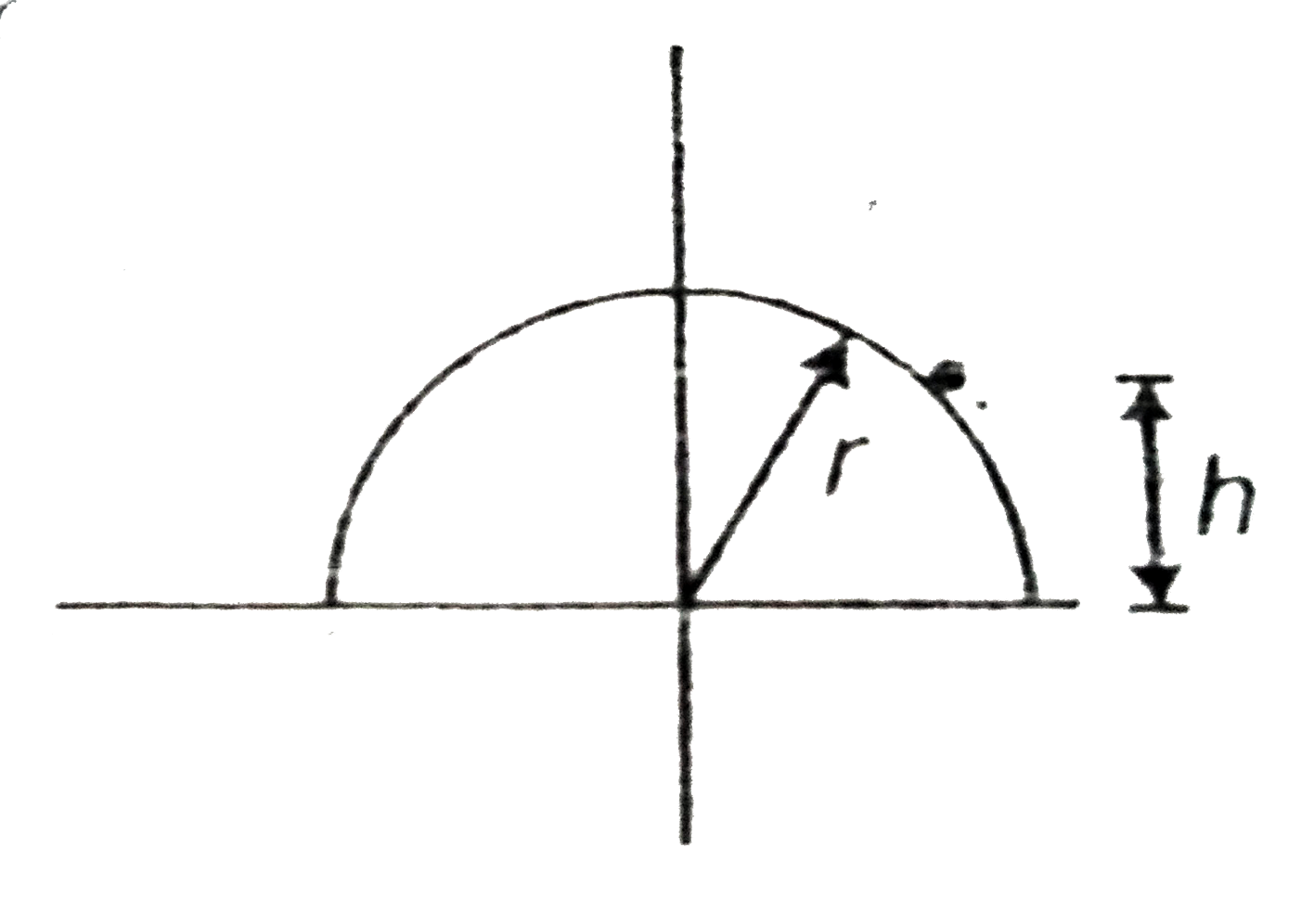 A32rB23rC12gt2Dv22g
A32rB23rC12gt2Dv22g - Question 3 - Select One
A particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'
.A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'
A particle of mass m is placed in equlibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical wheere cosθ35. if the work done against frictiion is 2mgR10x, find x.
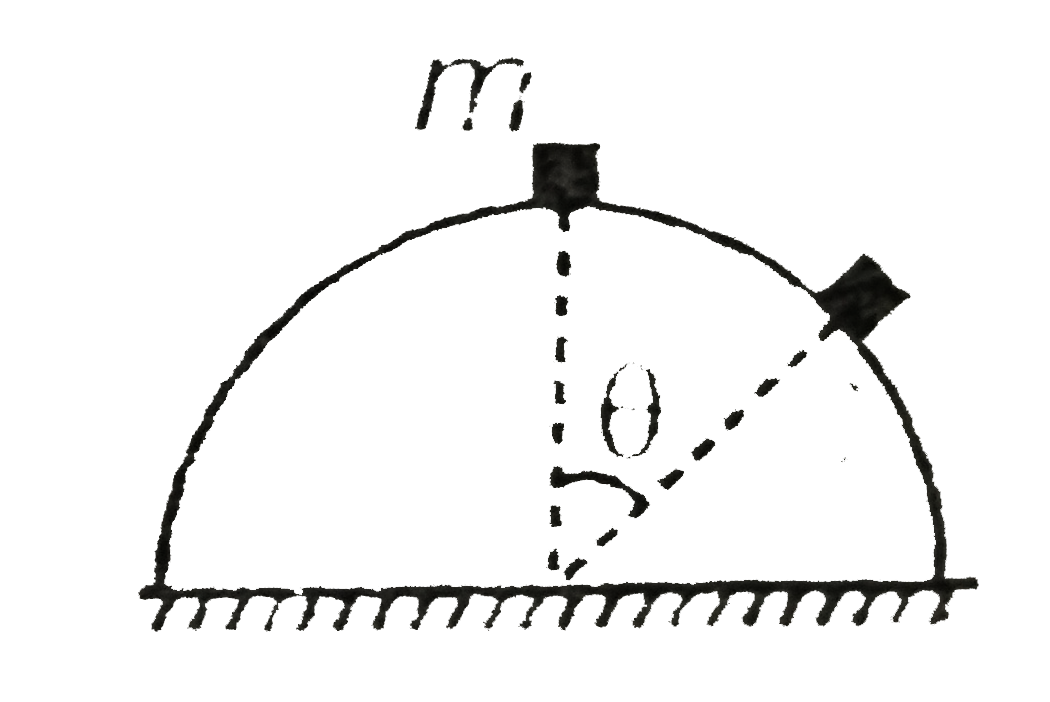 View Solution
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.
 View Solution
View SolutionA particle of mass m is released on a fixed. Smooth sphere of radius R at a position, where the radius through the particle makes an angle of α with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? (cosα=3/4)
View SolutionA particle of mass m slides down from the vertex of semi- hemisphere, without any initial velocity. At what height from horizontal will the particle leave the sphere-
View SolutionA hemisphere of radius R and mass 4 m is free to slide with its base on a smooth horizontal table . A particle of mass m is placed on the top of the hemisphere . The angular velocity of the particle relative to centre of hemisphere at an angular displacement θ when velocity of hemisphere has become v is
View Solution

