The escape velocity for a planet is ve. A particle starts from rest at a large distance from the planet, reaches the planet only under gravitational attraction, and passes through a smooth tunnel through its centre. Its speed at the centre of the planet will be
ve
1.5ve
√1.5ve
2ve
The correct Answer is:C
To solve the problem, we need to determine the speed of the particle when it reaches the center of the planet after starting from rest at a large distance. We will use the concept of conservation of energy.
1. Understanding Escape Velocity:
The escape velocity ve is the minimum velocity an object must have to escape the gravitational pull of a planet without any further propulsion. It is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
2. Initial Energy at Large Distance:
When the particle is at a large distance from the planet, it starts from rest, so its initial kinetic energy KEi is:
KEi=0
The gravitational potential energy PEi at a large distance is taken to be zero:
PEi=0
Therefore, the total initial energy Ei is:
Ei=KEi+PEi=0+0=0
3. Energy at the Center of the Planet:
When the particle reaches the center of the planet, its potential energy PEf can be calculated using the formula for gravitational potential energy inside a uniform sphere:
PE_f = -\frac{GMm}{R} \quad \text{(where m is the mass of the particle)}
The kinetic energy KEf at the center will be:
KEf=12mv2
where v is the speed of the particle at the center.
4. Applying Conservation of Energy:
According to the conservation of mechanical energy, the total energy at the beginning must equal the total energy at the center:
Ei=Ef
Therefore:
0=KEf+PEf
Substituting the expressions for KEf and PEf:
0=12mv2−GMmR
5. Solving for Speed v:
Rearranging the equation gives:
12mv2=GMmR
Dividing both sides by m (assuming m≠0):
12v2=GMR
Multiplying both sides by 2:
v2=2GMR
Taking the square root:
v=√2GMR
6. Relating to Escape Velocity:
We know that ve=√2GMR. Thus:
v=ve
Final Answer:
The speed of the particle at the center of the planet will be equal to the escape velocity ve.
The escape velocity ve is the minimum velocity an object must have to escape the gravitational pull of a planet without any further propulsion. It is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
When the particle is at a large distance from the planet, it starts from rest, so its initial kinetic energy KEi is:
KEi=0
The gravitational potential energy PEi at a large distance is taken to be zero:
PEi=0
Therefore, the total initial energy Ei is:
Ei=KEi+PEi=0+0=0
When the particle reaches the center of the planet, its potential energy PEf can be calculated using the formula for gravitational potential energy inside a uniform sphere:
PE_f = -\frac{GMm}{R} \quad \text{(where m is the mass of the particle)}
The kinetic energy KEf at the center will be:
KEf=12mv2
where v is the speed of the particle at the center.
According to the conservation of mechanical energy, the total energy at the beginning must equal the total energy at the center:
Ei=Ef
Therefore:
0=KEf+PEf
Substituting the expressions for KEf and PEf:
0=12mv2−GMmR
Rearranging the equation gives:
12mv2=GMmR
Dividing both sides by m (assuming m≠0):
12v2=GMR
Multiplying both sides by 2:
v2=2GMR
Taking the square root:
v=√2GMR
We know that ve=√2GMR. Thus:
v=ve
The speed of the particle at the center of the planet will be equal to the escape velocity ve.
Topper's Solved these Questions
Similar Questions
the escape velocity on a planet is v. if the radius of the planet contracts to 14 of the present value without any change in its mass, the escape velocity will be
View SolutionThe escape velocity from a planet is v0 The escape velocity from a planet having twice the radius but same density will be
View Solution
Knowledge Check
- Question 1 - Select One
The escape velocity for a planet is ve. A particle is projected from its surface with a speed v. For this particle to move as a satellite around the planet.
Ave2<v<veBve√2<v<veCve<v<√2veDve√2<v<ve2 - Question 2 - Select One
The escape velocity for a planet is ve. A particle is projected from its surface with a speed v. For this particle to move as a satellite around the planet,
Ave2<v<veBve√2<v<veCve<v<√2veDv√2<v<ve2 - Question 3 - Select One
A large solid sphere with uniformly distributed positive charge has a smooth narrow tunnel along its direction. A small particle with negative charge, initially at rest far from the sphere, approaches it along the line of the tunnel, reaches its surface with a speed v, and passes through the tunnel. Its speed at the centre of the sphere will be
A0B√1.5vC√2Dv
The escape velocity from a planet is v0. The escape velocity from a planet having twice the radius but same density will be
View SolutionNatural or artificial bodies that revolve around a planet under its gravitational force of attraction are called
View Solution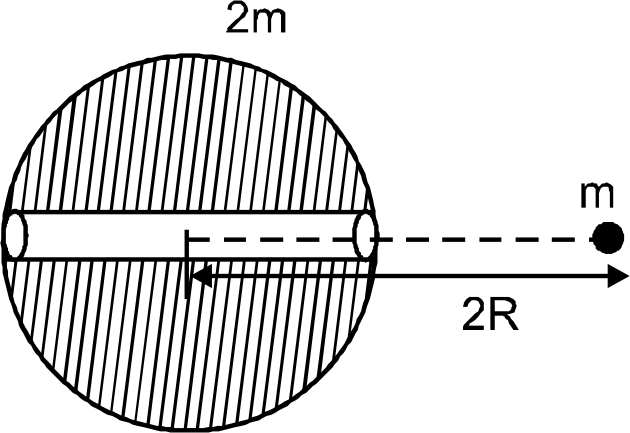
A solid spherical planet of mass 2m and radius 'R' has a very small tunnel along its diameter. A small cosmic particle of mass m is at a distance 2R from the centre of the planet as shown. Both are initially at rest, and due to gravitational attraction, both start moving toward each other. After some time, the cosmic particle passes through the centre of the planet. (Assume the planet and the cosmic particle are isolated from other planets)View SolutionThe escape velocity for a planet is ve. A tunnel is dug along a diameter of the planet and a small body is dropped into it at the surface. When the body reaches the centre of the planet, its speed will be
View SolutionIf the angular velocity of a planet about its own axis is halved, the distance of geostationary satellite of this planet from the centre of the centre of the planet will become
View Solution

