Two different masses m and 3m of an ideal gas are heated separately in a vessel of constant volume, the pressure P and absolute temperature T, graphs for these two cases are shown in the figure as A and B. The ratio of slopes of curves B to A is
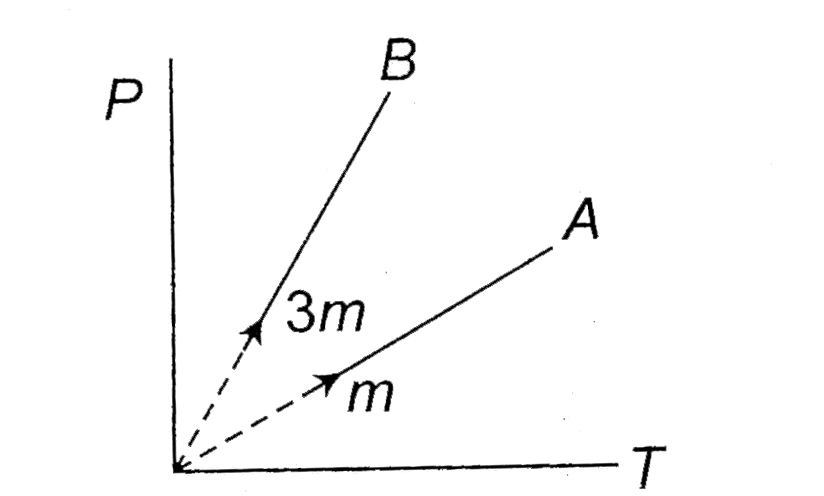
3:1
1:3
9:1
1:9
The correct Answer is:A
Slope =PT=nRV=MRM0V
(P/T)B(P/T)A=3mm=31
Topper's Solved these Questions
Similar Questions
m is the mass of a molecule, k is he Boltzmann constant,p is the pressure and T is the absolute temperature.The density of the gas is given by?
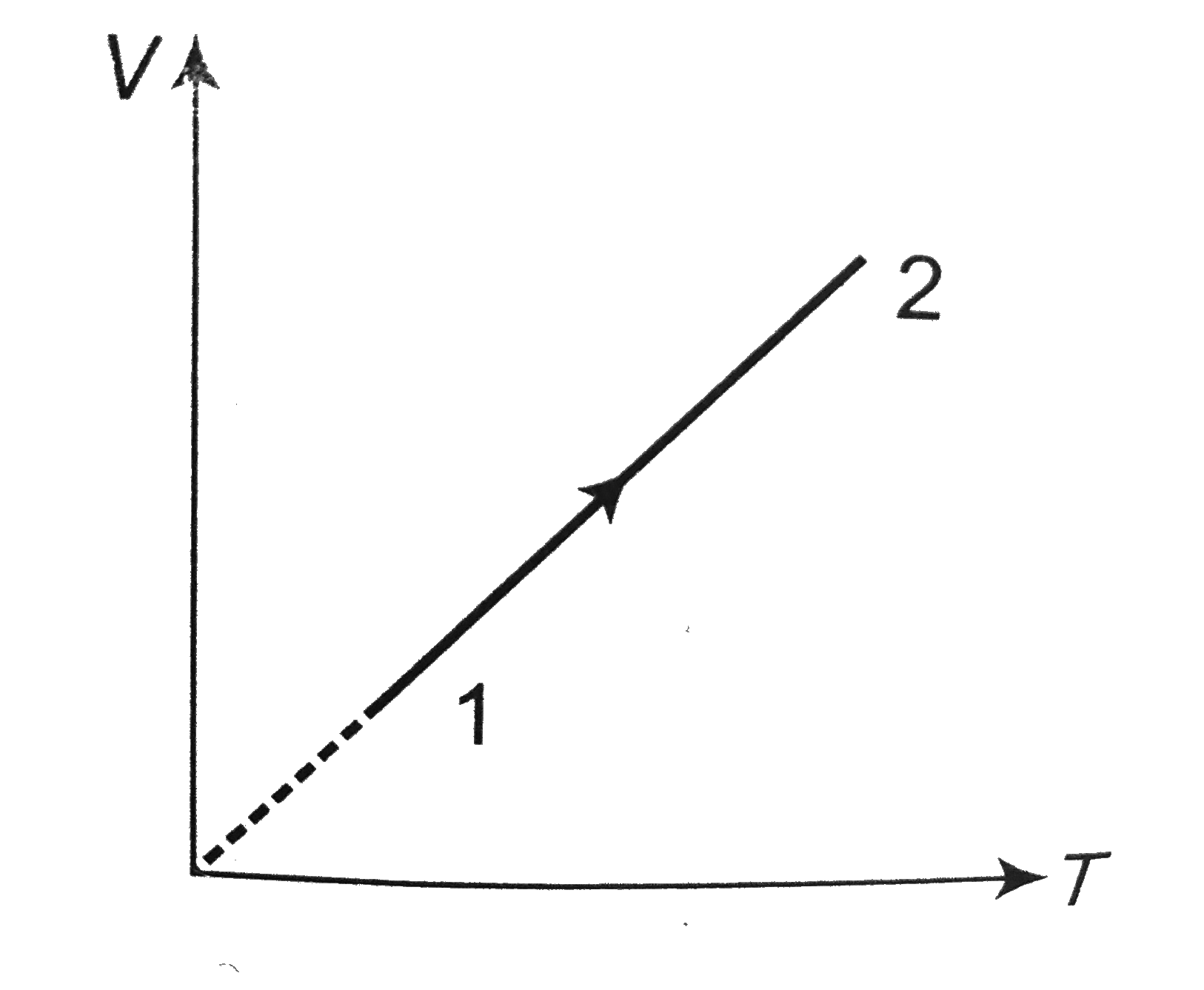
View SolutionVolume versus temperature graph of two moles of helium gas is as shown in figure. The ratio of heat absorbed and the work done by the gas in process 1−2 is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A sample of an ideal gas occupies a volume V at pressure P and absolute temperature T. The mass of each molecule is m, then the density of the gas is
AmKTBPmKTCPkmDPKT - Question 2 - Select One
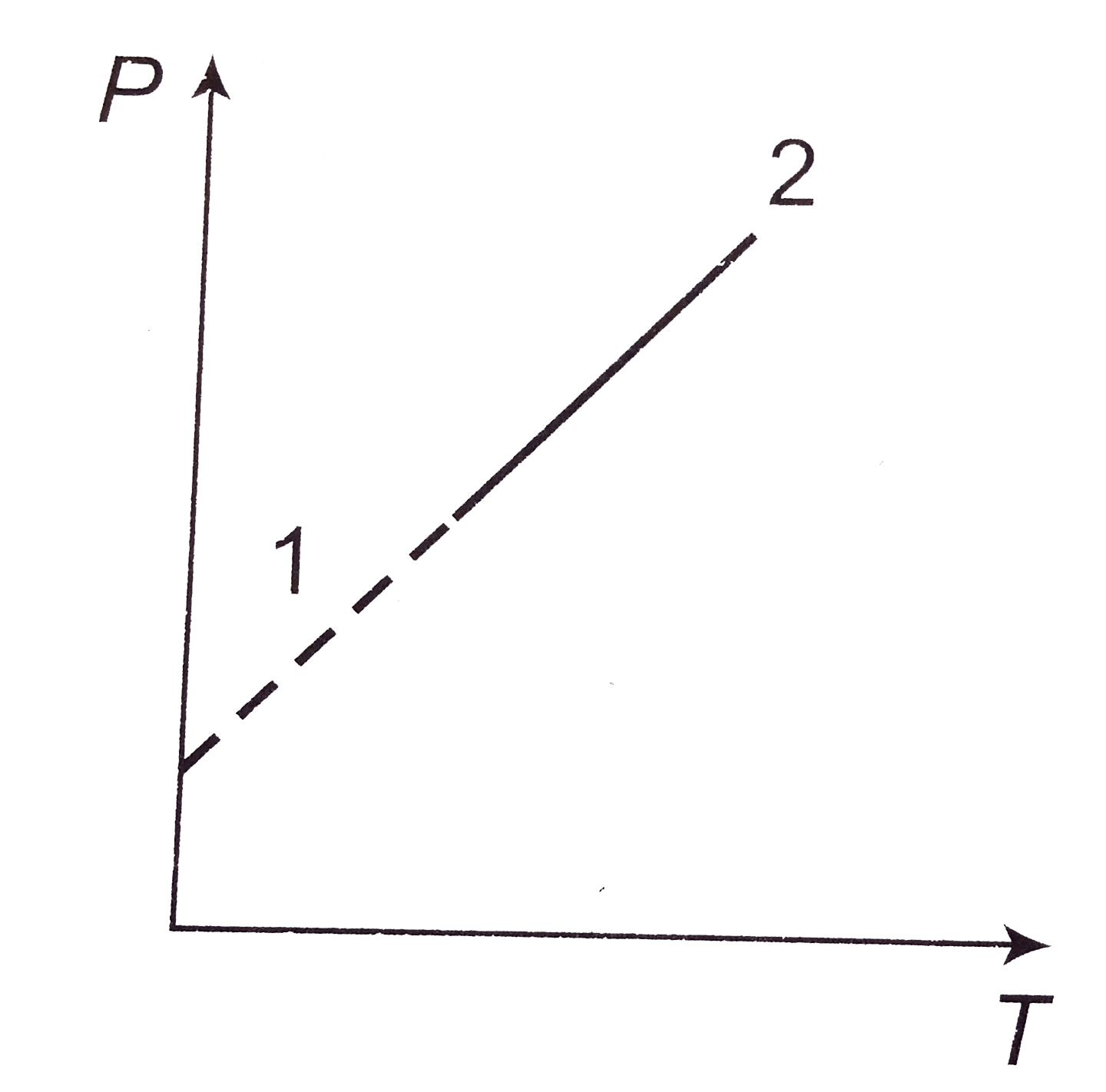
The P−T graph for the given mass of an ideal gas is shown in figure. Then the volume
_E01_022_Q01.png) AincreasesBdecreasesCremains constantDdata insuficient
AincreasesBdecreasesCremains constantDdata insuficient - Question 3 - Select One
A fiven sample of an ideal gas occupise a volume V at a pressure p and sbsoulte temperature T.The mass of each molecule of the gas is m. Which of the following fives the dinsity of the gas ?
AP/(kTV)BmkTCP/(kT)DPm/kT
A pressure P, absolute temperature T, graph was obtained whe a given mass of a gas heated. During the heating process from the state 1 to the state 2, the volumeView SolutionTwo vessels A and B contain the same gas. If the pressure, volume and absolute temperature of the gas in A are two times as compared to that in B, and if the mass of the gas in B is x grams, the mass of the gas in A will be
View SolutionA ideal gas has pressure 'p', volume 'V' and absolute temperature 'T'. It 'm' is the mass of each molecules and 'K' is the Boltzmann constant , the density of the gas is
View SolutionFigure shows the volume versus temperature graph for the same mass of a gas (assumed ideal) corresponding to two different pressure P1andP2. Then
View SolutionA diatomic gas undergoes same change of temperature by two different processes (i) at constant volume and (ii) at constant pressure. The heat supplied in the two cases will be in the ratio of
View Solution