The moment of inertia of a rod of length $l$ about an axis passing through its centre of mass and perpendicular to rod is $I$ . The moment of inertia of hexagonal shape formed by six such rods, about an axis passing through its centre of mass and perpendicular to its plane will be

Video Solution

Text Solution

Verified by Experts

$M . I .$ of rod $A B$ about its centre and perpendicular to length $= \frac{m l^{2}}{12} = I \Rightarrow m l^{2} = 12 I$

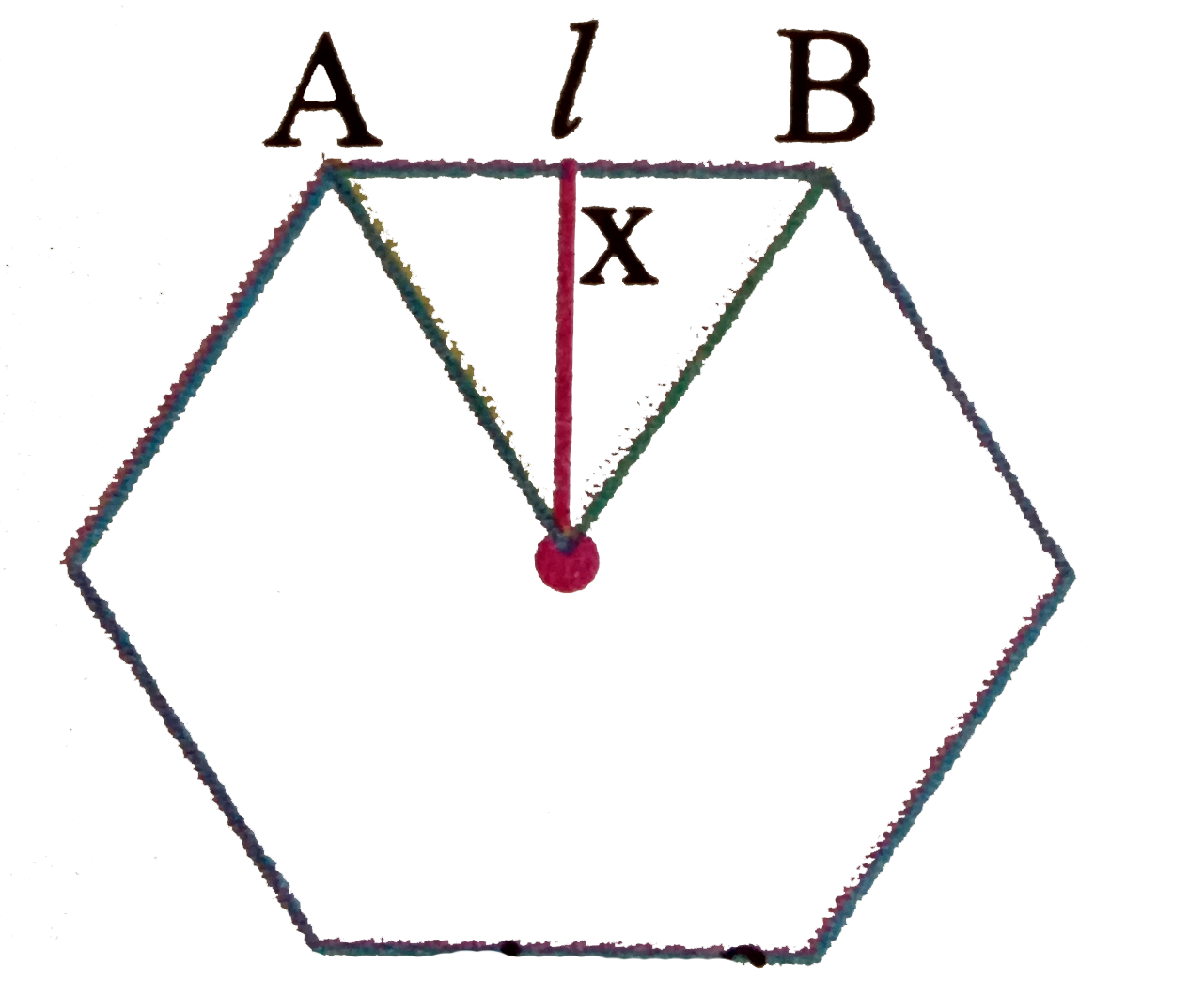
Now moment of inertia of rod about the axis which is passing through $O$ and perpendicular to the plane of hexagon
$I_{r o d} = \frac{m l^{2}}{12} + m x^{2}$ [from parallel axes theoram ]
$= \frac{m l^{2}}{12} + m {[\frac{\sqrt{3}}{2} l]}^{2} = \frac{5 m l^{2}}{6}$
Now moment of inertia of system
$I_{System} = 6 \times I_{r o d} = 5 m l^{2} = 5 \times 2 I = 60 I$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increased
Bchanges if its axis of rotation is changed
Cincreases if its angular velocity is increased
Dboth (a) and (b) are correct
Question 2 - Select One
The radius of gyration of an uniform rod of length $L$ about an axis passing through its centre of mass and perpendicular to its length is.
A $\frac{L}{\sqrt{2}}$
B $\frac{L^{2}}{\sqrt{12}}$
C $\frac{L}{\sqrt{3}}$
D $\frac{L}{\sqrt{2}}$
Question 3 - Select One
Moment of inertia of a solid cylinder of length L and diameter D about an axis passing through its centre of gravity and perpendicular to its geometric axis is
A $M (\frac{D^{2}}{4} + \frac{L^{2}}{12})$
B $M (\frac{L^{2}}{16} + \frac{D^{2}}{8})$
C $M (\frac{D^{2}}{4} + \frac{L^{2}}{6})$
D $M (\frac{L^{2}}{12} + \frac{D^{2}}{16})$

Recommended Questions

Home
Ask Doubt
Profile