The area of the triangle whose adjacent sides are represented by the vector $(4 ˆ i + 3 ˆ j + 4 ˆ k)$ and $5 ˆ i$ in sq. units is

A

$25$

B

$12.5$

C

$50$

D

$45$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Area of triangle $= \frac{1}{2} ∣ ∣ \to A \times \to B ∣ ∣$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-II(C.W.)
64videos
SYSTEM OF PARTICLES
BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-III
66videos
SYSTEM OF PARTICLES
BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - C.U.Q.
83videos
SYSTEM OF PARTICLES
BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10videos
PHYSICAL WORLD
BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION

Similar Questions

Knowledge Check

Question 1 - Select One
The cross product of two vectors gives a vector perpendicular to the plane containing the vectors.

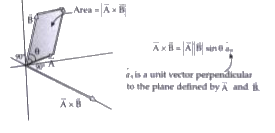
Area of parallelogram whose adjacent sides are represented by the vectors $\to a = 2 ˆ i - ˆ j + ˆ k$ and $\to b = 3 ˆ i - ˆ j$ is sq. units.
A3
B $\sqrt{10}$
C $\sqrt{11}$
D $2 \sqrt{3}$
Question 2 - Select One
The area of the parallelogram whose sides are represented by the vector $ˆ j + 3 ˆ k$ and $ˆ i + 2 ˆ j - ˆ k$ is
A $\sqrt{16} s q . u n i t$
B $\sqrt{59} s q . u n i t$
C $\sqrt{49} s q . u n i t$
D $\sqrt{52} s q . u n i t$

NARAYNA-SYSTEM OF PARTICLES-Level-1(C.W.)

Home
Ask Doubt
Profile