A solid sphere rolls down without slipping from rest on a 30∘ incline. Its linear acceleration is
5g/7
5g/14
2g/3
g/3
The correct Answer is:B
a=gsinθ1+k2R2
Topper's Solved these Questions
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-II(C.W.)
64 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-III
66 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - C.U.Q.
83 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
Similar Questions
An inclined plane makes an angle 30° with the horizontal. A solid sphere rolling down this inclined plane from rest without slipping has a linear acceleration equal to
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m.

Linear velocity of first sphere after it again starts rolling without slipping is:
View Solution
Knowledge Check
An inclined plane makes an angle 30° with the horizontal. A solid sphere rolling down this inclined plane from rest without slipping has a linear acceleration equal to
Ag3B2g3C5g7D5g14A solid sphere rolls without slipping down a 30∘ inclined plane. If g=10ms−2 then the acceleration of the rolling sphere is
A5ms−2B725ms−2C257ms−2D157ms−2A solid sphere rolls down without slipping on an inclined plane at angle 60∘ over a distance of 5 m. The acceleration (in ms−2) is
A5.23B7.07C6.06D3.23
A uniform solid sphere rolls down an incline. (a) What must be the incline angle if the linear acceleration of the center of the sphere is to have a magnitude of 0.15 g? (b) If a frictionless block were to slide down the incline at that angle, would its acceleration magnitude be more than, less than or equal to 0.15 g? Why?
View SolutionA sphere of mass m rolls without slipping on a plane inclined at θ. The linear acceleration of the sphere will be 57gsinθ. The minimum value of μ for this to be possible is
View SolutionA solid spherical ball is rolling without slipping down an inclined plane. The fraction of its total kinetic energy associated with rotation is
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
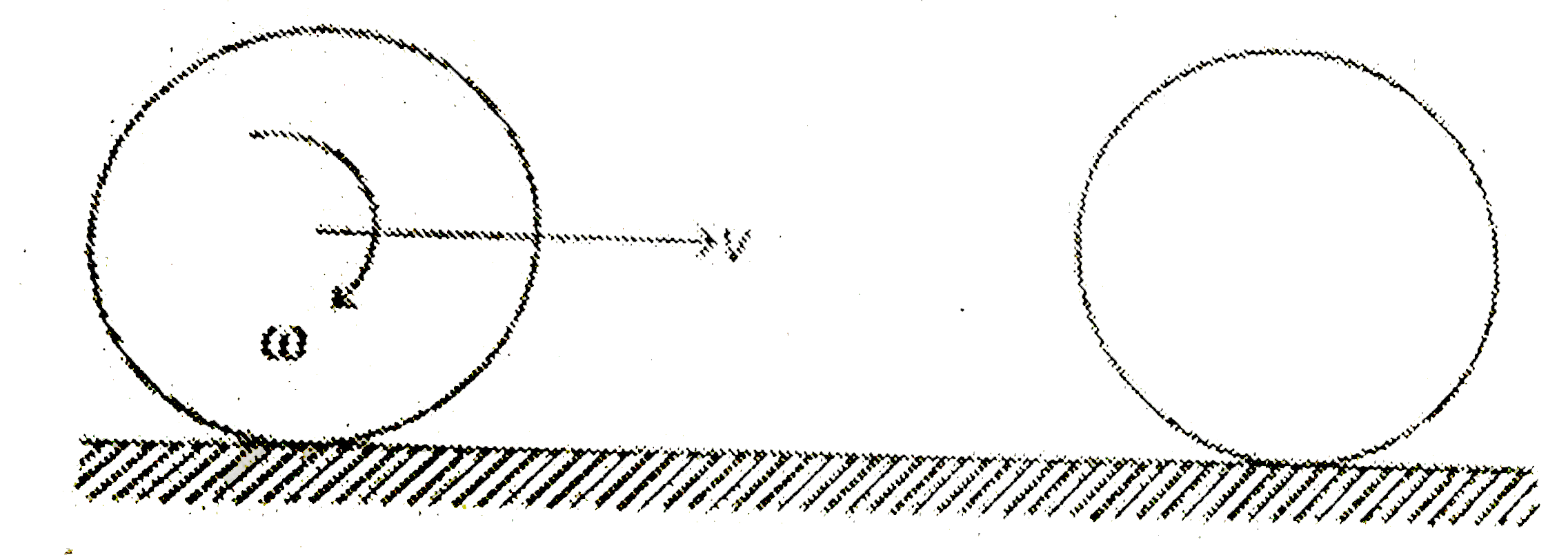
Linear velocity of first sphere after it again starts rolling without slipping is
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View Solution