A rod touches a disc kept on a smooth horizontal plane. If the rod moves with an acceleration a, the disc rolls on the rod without acceleration a, the disc rools on therod without slidding. Then , the acceleration of the disc w.r.t the rod is

a3
√3a2
zero
a/2
The correct Answer is:A
macosθ−f=mA→(1)
f×r=Iα→(2),A=rα→(3)
From about equation A=a3
A=a3 (where θ=60∘&I=12mr2)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -II(H.W)47videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
View SolutionA string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
View Solution
Knowledge Check
- Question 1 - Select One
A block slides down a plane. Inclined at 30∘ to the horizontal, with an acceleration a. A disc rolling without slipping down the same inclined plane would have an acceleration
A13 aB12 aC23 aD57 a - Question 2 - Select One
A force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:
 A2F3mB10F7mCzeroD4F3m
A2F3mB10F7mCzeroD4F3m - Question 3 - Select One
A bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a0 in a direction forming angle θ with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is
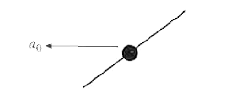 AgsinθB(g+a0)sinθCgsinθ+a0cosθDgsinθ−a0cosθ
AgsinθB(g+a0)sinθCgsinθ+a0cosθDgsinθ−a0cosθ
A disc roll on an inclined plane without slipping Rotational and total energy is
View SolutionThe point P of a string is pulled up with an acceleration g. Then the acceleration of the hanging disc (w.r.t ground) over which the string is wrapped, is
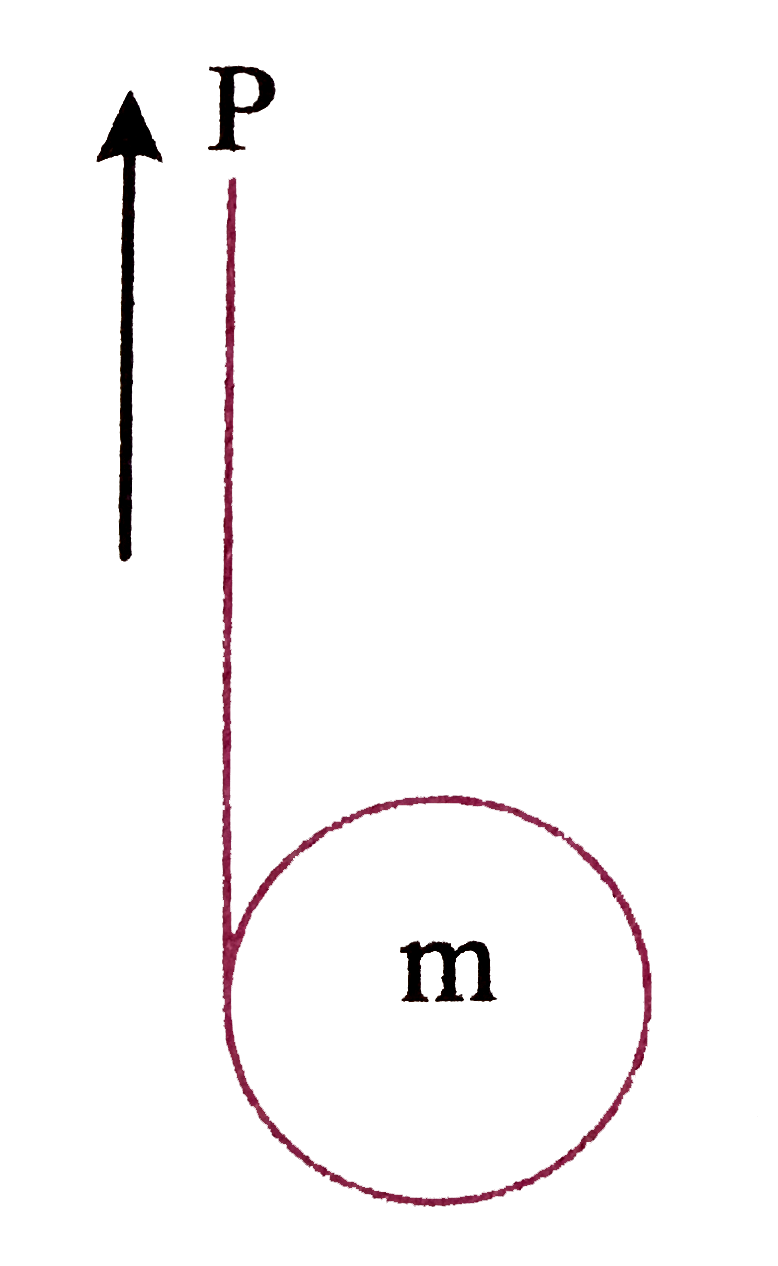 View Solution
View SolutionTwo solid discs of radii r and 2r roll from the top of an inclined plane without slipping. Then
View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
zView SolutionA solid sphere slides down a smooth inclined plane of inclination θ with acceleration a1. A disc rolls down a rough inclined plane of inclination θ with acceleration a2. Value of a1a2 is
View Solution

