A string is wrapped several time on a cylinder of mass M and radius R, the cylinder is pivoted about its axis of symmetery . A block mass of m tied to the string rests on support so that the string is black. The block is lifted upto a height h and the support is removed. (shown in figure)
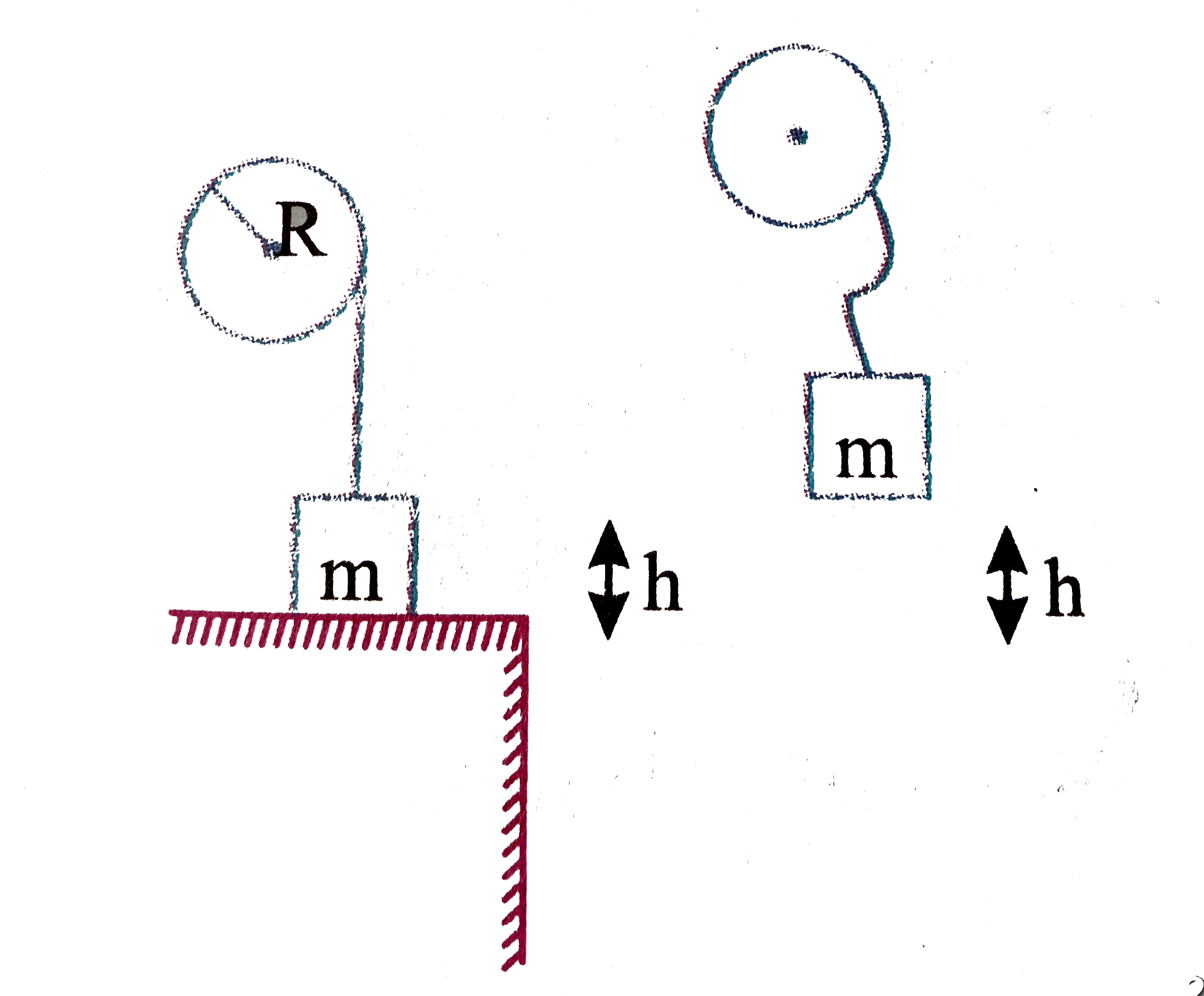
When the string experience a jerk, a large impulsive force is generated for a short duration, so that contribution of weight mg can be neglected suring this duration. then what will be speed of blocks m, just after string has becomes taut
√2gh[1+Mm]
√2gh[1+M2m]
√gh[1+Mm]
√gh[1+M2m]
The correct Answer is:B
When the string experiences a jerk, the large impulse developed is of very short duration so that the contribution of weight mg can be neglected during this time interval. The angular momentum of the system is conserved, as the tension is internal force for the system. thus we have →Li=→Lf
mv1R+12MR2ω1=mv0R=m√2ghR
The string is inextensible, so v1=Rω1. on solving for ω1 we get ω1=√2ghR[1+(M/2m)]
v1=Rω1=√2gh[1+(M/2m)]
the final kinetic energy K1 is given by
K1=12mv21+12Iω21=12mv21+12(12MR2)(v21R2)
=12(m+M2)v21=12[mv201+(M/2m)]
=K01+(M/2m),{:'Ko=12mv20}
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -II(H.W)47videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
 View Solution
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upward to prevent the centre of mass from falling as the string unwinds. Assume that the cylinder remains horizontal throughout and the thread does not slip. Find the length of the string unwound when the cylinder has reached an angular speed ω.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A string is wrapped several time on a cylinder of mass M and radius R, the cylinder is pivoted about its axis of symmetery . A block mass of m tied to the string rests on support so that the string is black. The block is lifted upto a height h and the support is removed. (shown in figure)
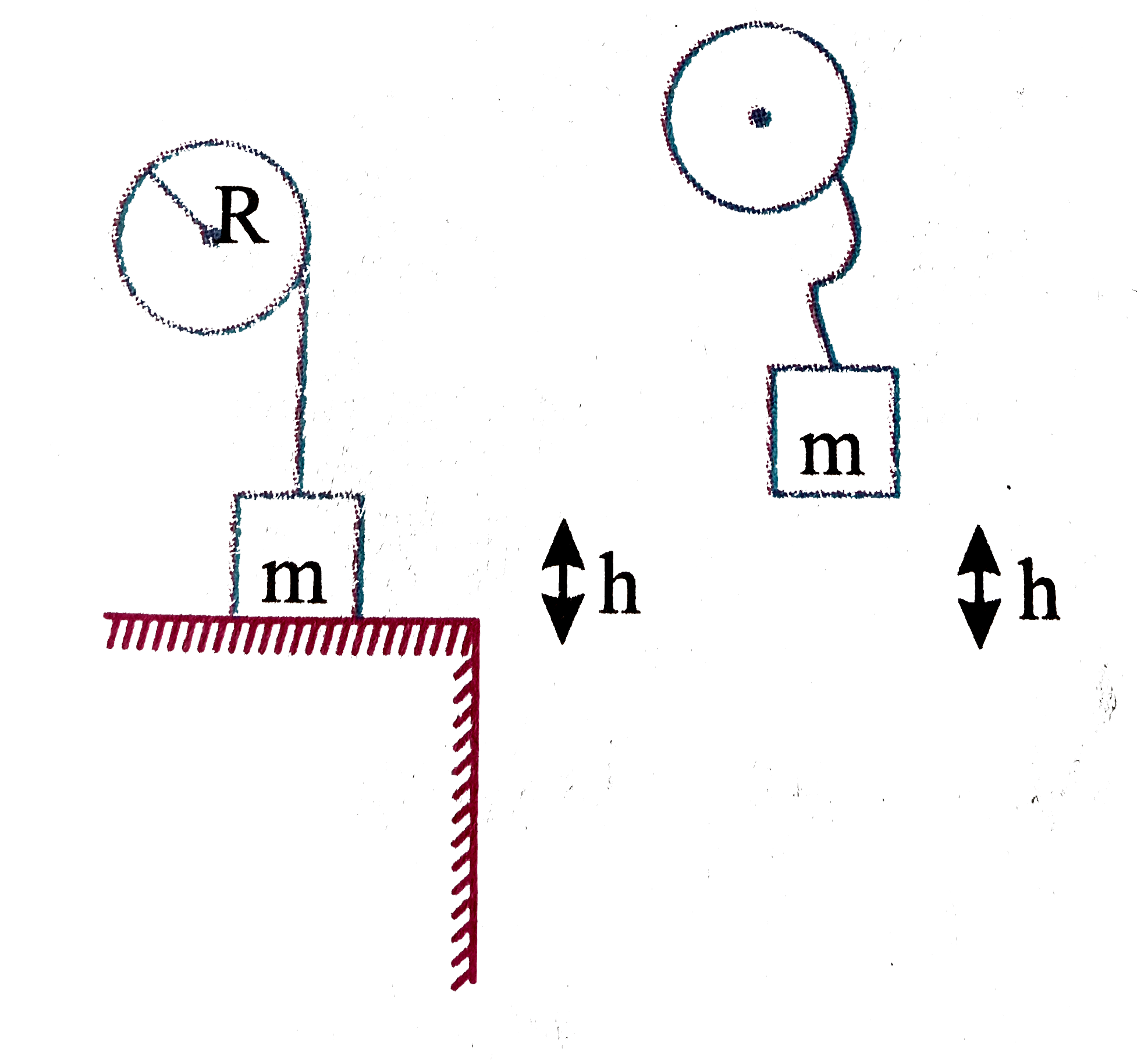
If M=m, what friction of KE is lost due to the jerk developed in the stringA1/2B2/3C1/3D1/4 - Question 2 - Select One
A string is wrapped several time on a cylinder of mass M and radius R, the cylinder is pivoted about its axis of symmetery . A block mass of m tied to the string rests on support so that the string is black. The block is lifted upto a height h and the support is removed. (shown in figure)
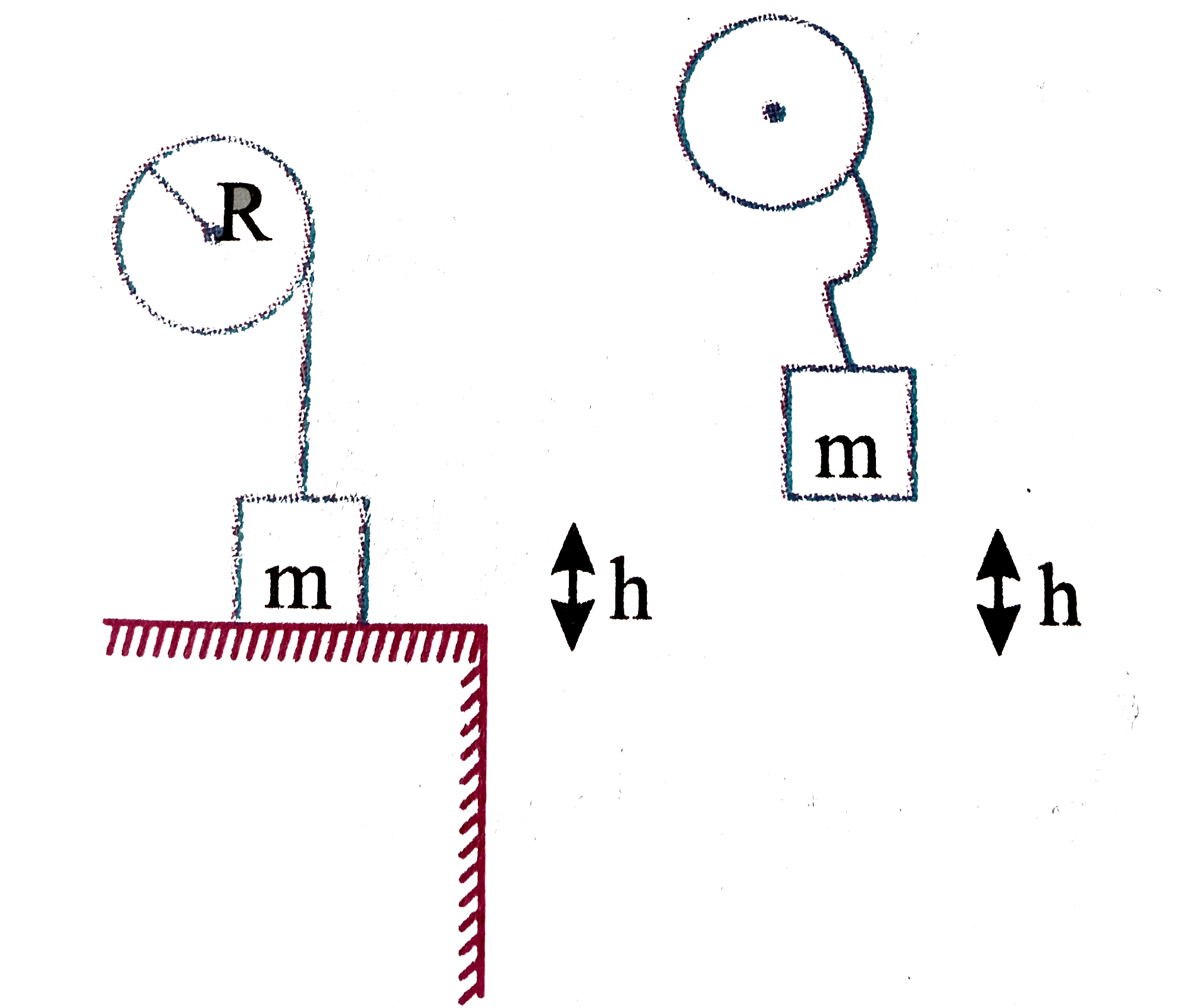
What is the angular velocity of cylinder just before the string becomes tautAzeroB√2ghRC√ghRD√ghR - Question 3 - Select One
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
A2Mg/3BMg/2CMg/3DMg/6
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
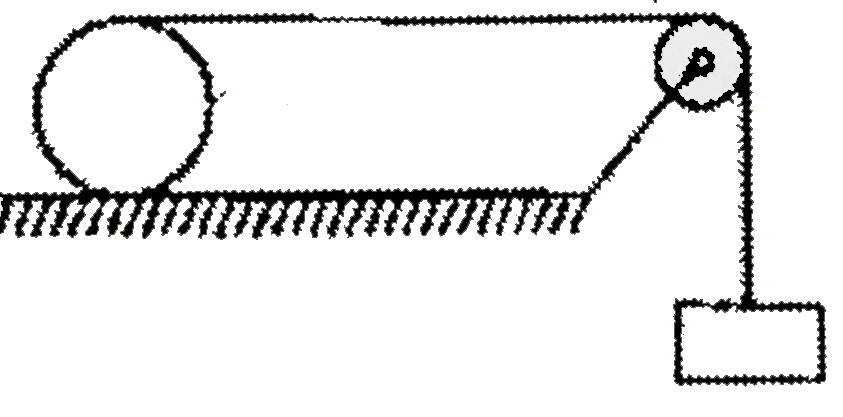
Acceleration of cylinder is:View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
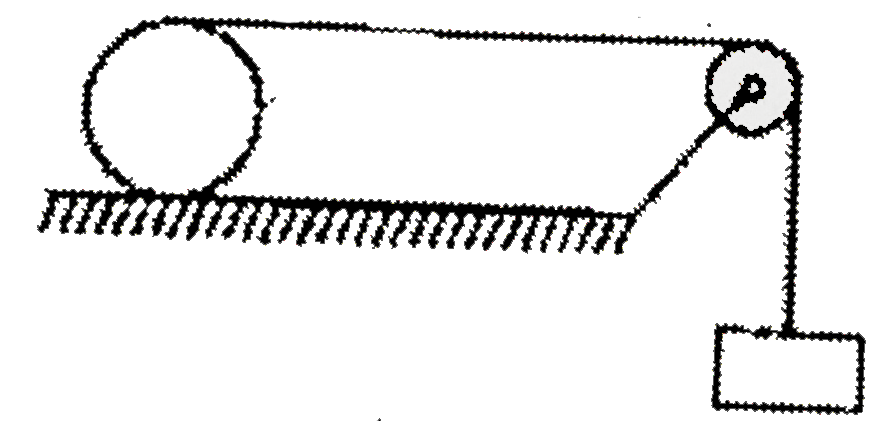
Velocity of point of contact 'of cylinder at this moment is:View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
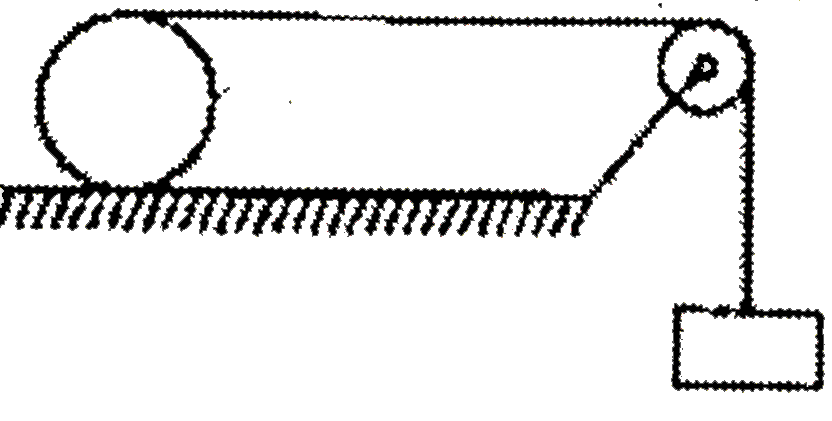
Acceleration of hanging mass is:View Solution

