A lift is tied with thick iron wire and its mass is 1000kg. If the maximum acceleration of the lift is 1.2ms2 and the maximum stress of the wire is 1.4×108Nm2 what should be the minimum diameter of the wire?
10−2m
10−4m
10−6m
0.5×10−2m
The correct Answer is:A
To solve the problem, we need to find the minimum diameter of the iron wire that can support a lift with a mass of 1000 kg, given the maximum acceleration and maximum stress. Here’s a step-by-step solution:
Step 1: Identify the given values
- Mass of the lift (m) = 1000 kg
- Maximum acceleration (a) = 1.2 m/s²
- Maximum stress (σ) = 1.4 × 10⁸ N/m²
- Acceleration due to gravity (g) = 9.8 m/s² (approximately)
Step 2: Calculate the total force acting on the wire
The total force (F) acting on the wire when the lift is accelerating upwards can be calculated using the formula:
F=m(g+a)
Substituting the known values:
F=1000kg×(9.8m/s²+1.2m/s²)
F=1000kg×11m/s²
F=11000N
Step 3: Relate stress to force and area
Stress (σ) is defined as the force (F) per unit area (A):
σ=FA
The area (A) of the wire can be expressed in terms of its radius (r):
A=πr2
Thus, we can rewrite the stress equation as:
σ=Fπr2
Step 4: Rearrange the equation to find r
From the stress equation, we can solve for the radius (r):
r2=Fπσ
Substituting the values of F and σ:
r2=11000Nπ×1.4×108N/m²
Step 5: Calculate r²
Calculating the denominator:
π×1.4×108≈4.398×108N/m²
Now substituting this into the equation for r²:
r2=110004.398×108
r2≈2.5×10−5m2
Step 6: Calculate r
Taking the square root to find r:
r≈√2.5×10−5
r≈0.005m
Step 7: Calculate the diameter
The diameter (d) is twice the radius:
d=2r
d≈2×0.005m=0.01m
Thus, the minimum diameter of the wire is:
d=10mm
Final Answer
The minimum diameter of the wire should be 10 mm.
- Mass of the lift (m) = 1000 kg
- Maximum acceleration (a) = 1.2 m/s²
- Maximum stress (σ) = 1.4 × 10⁸ N/m²
- Acceleration due to gravity (g) = 9.8 m/s² (approximately)
The total force (F) acting on the wire when the lift is accelerating upwards can be calculated using the formula:
F=m(g+a)
Substituting the known values:
F=1000kg×(9.8m/s²+1.2m/s²)
F=1000kg×11m/s²
F=11000N
Stress (σ) is defined as the force (F) per unit area (A):
σ=FA
The area (A) of the wire can be expressed in terms of its radius (r):
A=πr2
Thus, we can rewrite the stress equation as:
σ=Fπr2
From the stress equation, we can solve for the radius (r):
r2=Fπσ
Substituting the values of F and σ:
r2=11000Nπ×1.4×108N/m²
Calculating the denominator:
π×1.4×108≈4.398×108N/m²
Now substituting this into the equation for r²:
r2=110004.398×108
r2≈2.5×10−5m2
Taking the square root to find r:
r≈√2.5×10−5
r≈0.005m
The diameter (d) is twice the radius:
d=2r
d≈2×0.005m=0.01m
Thus, the minimum diameter of the wire is:
d=10mm
The minimum diameter of the wire should be 10 mm.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-III29videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - NCERT BASED QUESTIONS21videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-I (C.W)37videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - III30videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)31videos
MOTION IN A PLANE
Similar Questions
A lift is tied with a thick iton wires and its mass is 800 kg. if the maximum ac celeration of lift is 2.2ms−2 and the maximum safe stress is 1.4×108Nm−2 find the minimum diameter of the wire take g=9.8ms−2
View SolutionA lift of mass 2000 kg is supported by thick steel ropes . If maximum upward acceleration of the lift be 1.2m/s2 , and the breaking stress for the ropes be
2.8×108Nm−2
what should be the minimum diameter of rope ?View Solution
Knowledge Check
- Question 1 - Select One
A lift is tied with thick iron and its mass is 314 kg. What should be the minimum diameter of wire if the maximum acceleration of lift is 1.2msec2 and the maximum safe stress of the wire is 1×107Nm2?
A2 cmB1 cmC1.5 cmDnone of these - Question 2 - Select One
A lifts is tied with thick iron wires and its mass is 1000 kg. The minimum diameter of wire, If the maximum accelertion of lifts is 1.2m/s2 , is ( g =9.8m/s2)
A0.00141 mB0.00282 mC0.005 mD0.01 m - Question 3 - Select One
Two blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
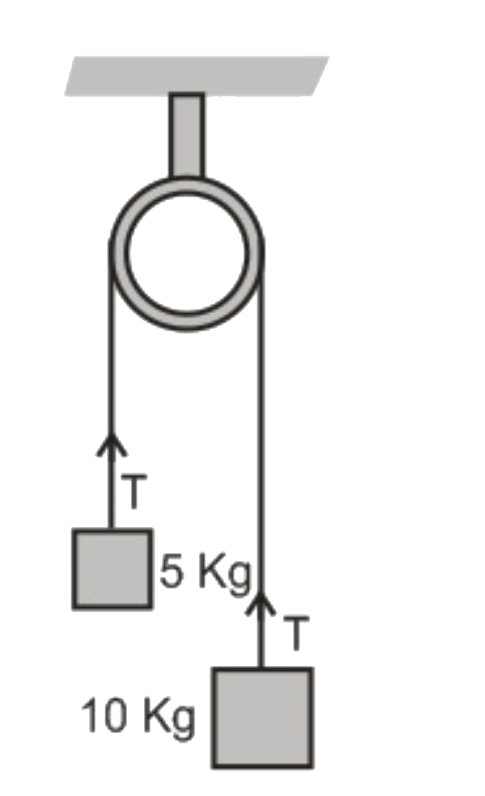 A0.1 mmB0.2 mmC0.05 mmD0.25 mm
A0.1 mmB0.2 mmC0.05 mmD0.25 mm
A rocket with a lift mass of 10,000 kg is blasted upwards with an acceleration of 10ms−2. Calculate the initial thrust of the blast
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
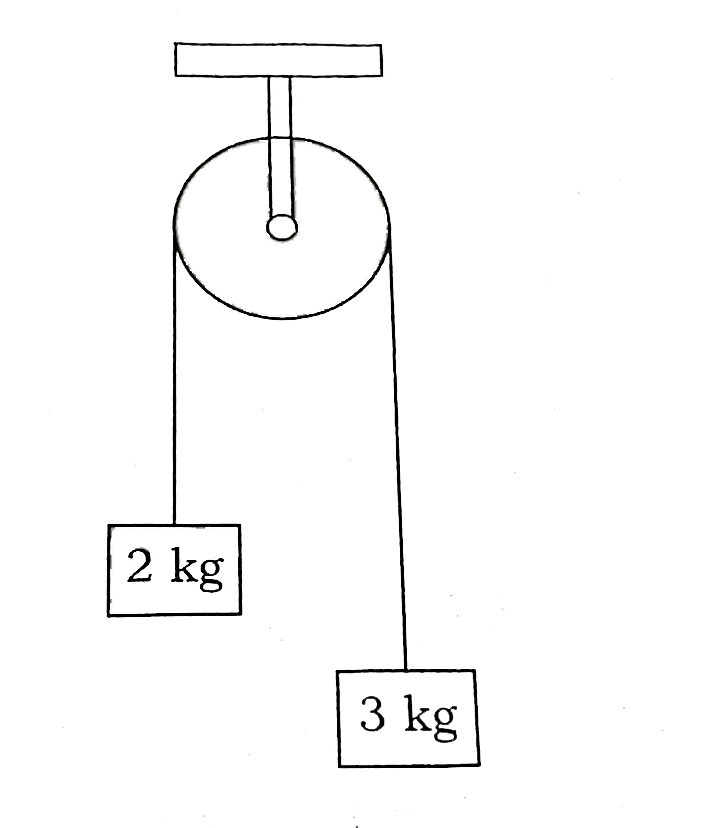 View Solution
View SolutionThe maximum load that may be applied to a mild steel wire is 7 kg wt. If the radius of the wire is 0.2 mm, find the maximum elastic strain permitted . [Y=2×1011N/m2]
View SolutionThe density of the material of a wire used in sonometer is 75×10−2kg/m3. If the stress on the wire is 3.0×104N/m2, the speed of transverse wave in the wire will be
View SolutionA lift of mass 'm' is connected to a rope which is moving upward with maximum acceleration 'a'. For maximum safe stress, the elastic limit of the rope is 'T'. The minimum diameter of the rope is
(g = gravitational acceleration)View Solution

