If the ratio of lenghts, radi and Young's moduli of steel and brass wires are a,b and c respectively their respective loads are in the ratio 3:2 then the corresponding ratio of increases in their lenghts would be
2a2cb
3a2b2c
3acb2
3c2ab2
The correct Answer is:B
Δl=FLAY⇒ΔlSΔlB=(FSFB)(LSLB)(ABAS)(YBYS)
=(32)(a)(1b2)(1c)=3a2b2c
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - NCERT BASED QUESTIONS21videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - SINGLE ANSWER TYPE15videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (C.W)32videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - III30videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)31videos
MOTION IN A PLANE
Similar Questions
If the ratio of lengths, radii and young's modulii of steel and brass wires in the figure are a,b and c, respectively. Then, the corresponding ratio of increase in their lengths would be
 View Solution
View SolutionIf the ratio of diameter, lengths and Young's modulus of steel and brass wires shown in figure are 2 : 1, 2 : 1 and 2 : 1 respectively, then the corresponding ratio of increase in their lengths would be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c respectively then the corresponding ratio of increase in their lengths is
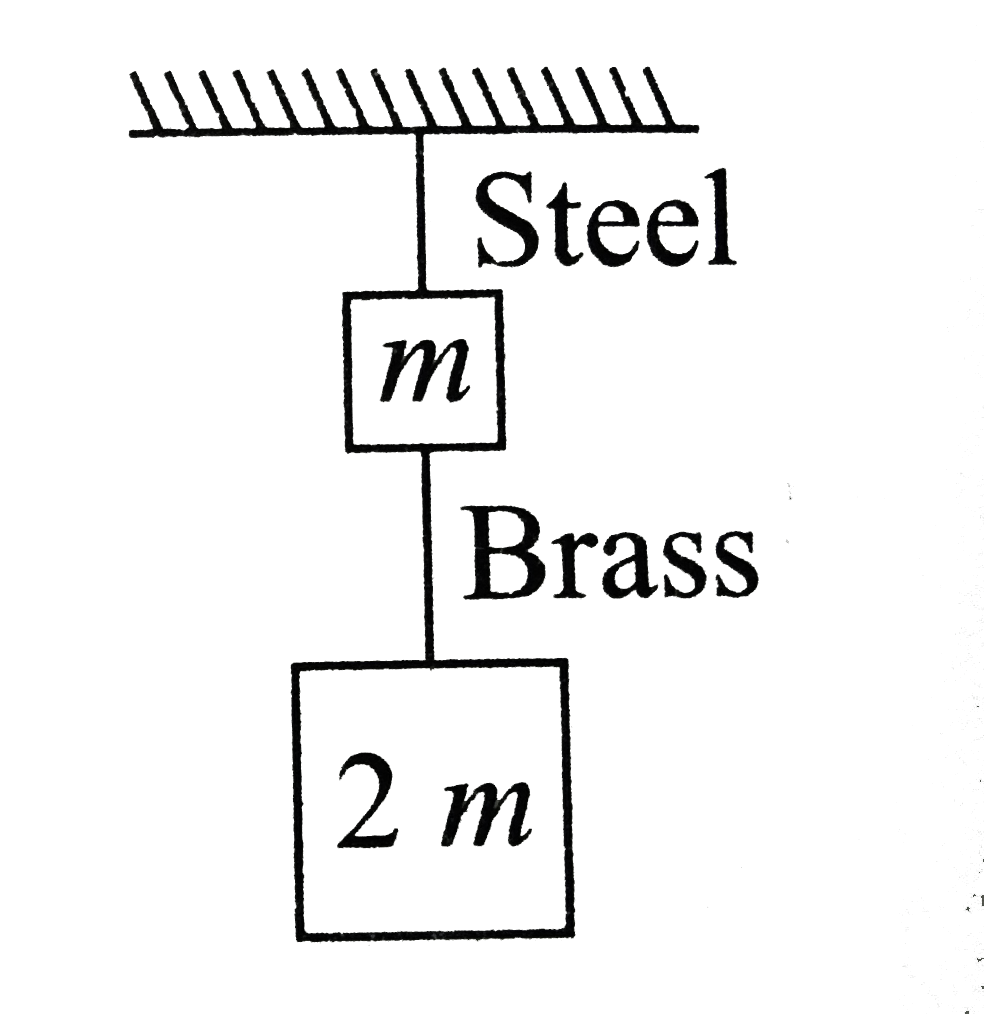 A2a2cbB3a2b2cC2acb2D3c2ab2
A2a2cbB3a2b2cC2acb2D3c2ab2 - Question 2 - Select One
If the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c repectively then the corresponding ratio of increase in their lengths is
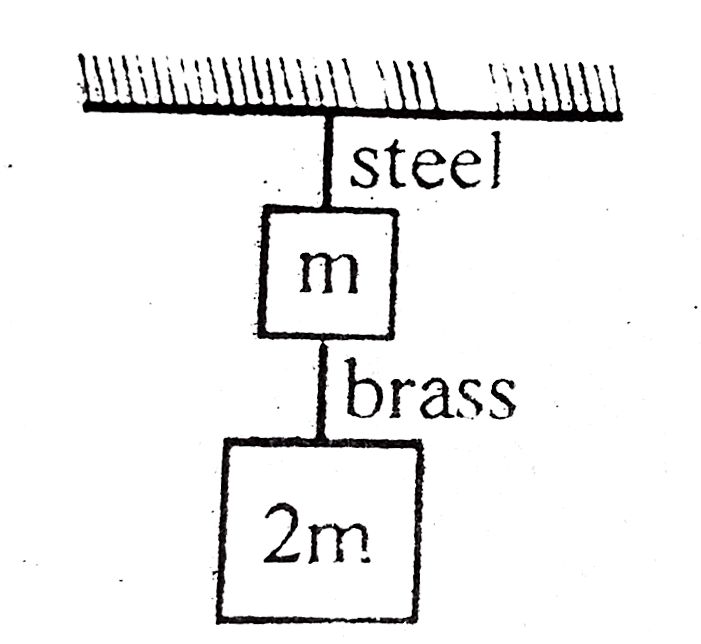 A2a2c/bB3a/2b2cC2ac/b2D3c/2ab2
A2a2c/bB3a/2b2cC2ac/b2D3c/2ab2 - Question 3 - Select One
If the ratio of diameters,lengths and Young's moduli of steel and brass wires shown in the figure are p, q and r respectively . Then the corresponding ratio of increase in their lenghts would be
 A3q5p2rB5q3p2rC3q5prD5q3pr
A3q5p2rB5q3p2rC3q5prD5q3pr
If the ratio of lengths, radii and youngs's modulus of steel and and brass wires in figure are 2:1,2:1,3:1 respectively. Then corresponding ratio of increases in their would be. (Neglect the mass of the wire and take g=10m/s2)
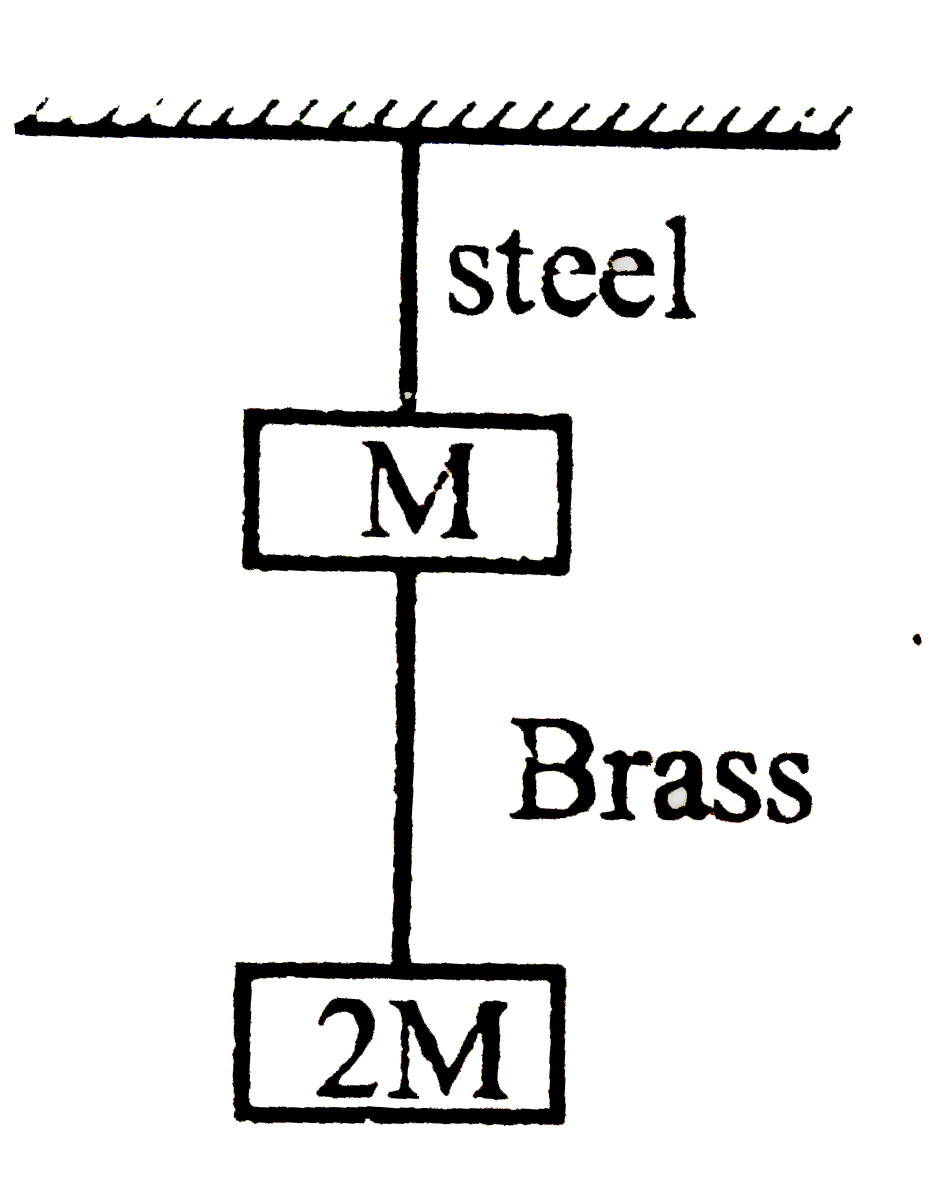 View Solution
View Solution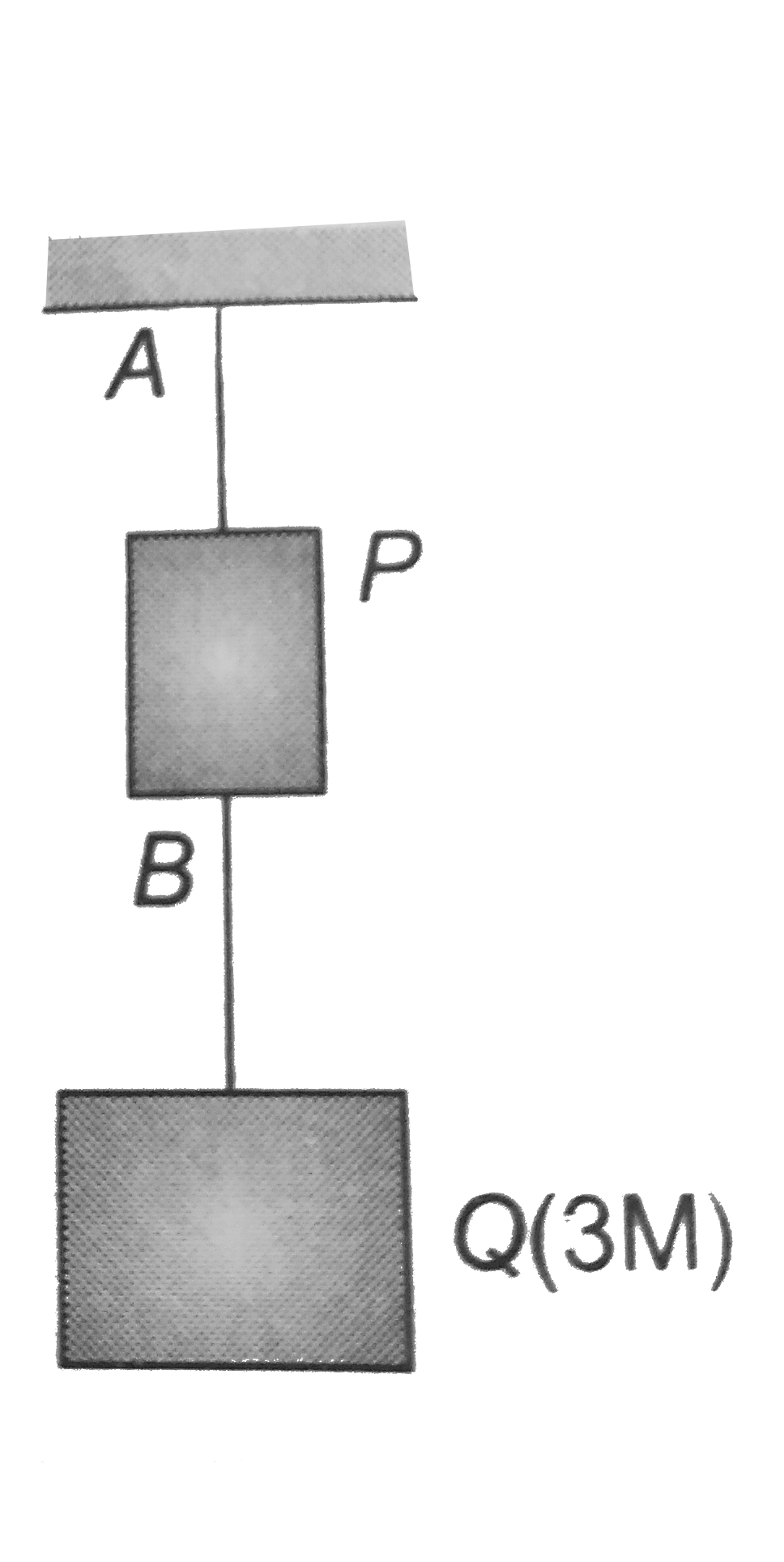
Wires A and B are connected with blocks P and Q, as shown, the ratio of lengths radii and Young's modulus of wires A and B are r, 2r and 3r respectively (r is a constant). Find the mass of block P if ratio of increase in their corresponding length is 16r2. The mass of the block Q is 3MView SolutionTwo wires of different materials having Young's moduli in the ratio 3:5, lengths in the ratio 2:1 and diameters in the ratio 1:2 are stretched with the same force. The ratio of stress in the wires is
View SolutionTwo wires of different materials having Young's moduli in the ratio 3:5, lengths in the ratio 2:1 and diameters in the ratio 1:2 are stretched with the same force. The ratio of stress in the wires is
View SolutionThe radii and Young's moduli of two uniform wires A and B are in the ratio 2:1 and 1:2 respectively. Both wires are subjected to the same longitudinal force. If the increase in leangth of the wire A is one percent, the percentage increae in length of the wire B is
View Solution

