Question

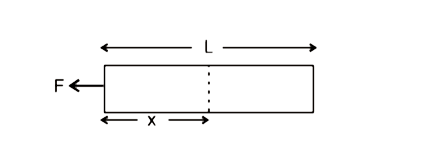
A rod of length $l$, mass $M$, cross section area $A$ is placed on a rough horizonatal surface. A horizonatal force $F$ is applied to rod as shwon in figure. The coefficient of fricition between rod and surface is $\mu$, the Young, modulus of material of rod is $Y$. [Assume that fricition force is distributed uniformly on rod]

The elongation in the rod if $F<\mu Mg$ is

Options

A. Zero
B. `[(F- (mu Mg)/(2))/(2AY)]l`
C. `(Fl)/(2AY)`
D. None

Answer

C

Explanation

Then, `F-T - f_(1) = 0 & T = f_(2)`
where `f_(1) + f_(2) = f = F`
As friction force is distributed uniformly, `f_(1) = (fx)/(l)`
`rArr T = F - f_(1) = F (f xx x )/(l) = F [1 - (x)/(l)]`
Let `Delta (dx)` be the elongation in `dx` lenghth of rod
`Delta (dx)` be the elongation in `dx` lenghth of rod
`Delta (dx) = (Tdx)/(Ay) = (F(1 - (x)/(l))dx)/(AY)`
Total elongation,
`Delta L = int Delta (dx) = int_(0)^(1) (F)/(AY) (1 - (x)/(l))dx = (Fl)/(2YA)`