A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,
,
1.35N
1.55N
1.65N
1.75N
The correct Answer is:A
In equilibrium total weight W=Kx+Fb
(M+m)g=Kx+Vρwg
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Statement Type Questions
16 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - More Than One Alternative Type Question
32 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 2 (C.W)
40 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,
,
View SolutionA spring is attached to a wooden cubical block of edge 5cm and placed in a water conatiner as shown in figure. Calculate the maximum weight to be placed on the block so that it is just immersed in water completely. Density of wood =700kg/m3, spring constant of spring =70N/m,g=10m/s2. Assume that initially spring is in its normal length.

View Solution
Knowledge Check
A cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
Aa(a2ρg+k)Ba(aρg+2k)Ca(aρg2+2k)Da(a2ρg+k2)A cubical block of side 0.5 m floats on water with 30% of its volume under water. What is the maximum weight that can be put on the block without fully submerging it under water?
[Take, density of water =103kg/m3]A87.5 kgB30.1 kgC46.3 kgD65.4 kgFrom the fixed pulley, masses 2 kg, 1 kg and 3 kg are suspended as shown is figure. Find the extension in the spring when acceleration of 3 kg and 1 kg is same if spring constant of the spring k = 100 N/m. (Take g=10ms−2)
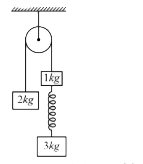 A10 cmB20 cmC30 cmD25 cm
A10 cmB20 cmC30 cmD25 cm
A cubical block 'A' of mass m0(=a3ρ=3kg) of edge 'a' and density ρ floats in a liquid of density 3ρ. The lower surface of the cube just touches the free end of massless spring of spring of spring constant k(=a2ρg) fixed at the bottom of the vessel. Another block 'B' of mass 'm' is lept over block 'A', so that is completely immersed in liquid without wetting the block 'B'. Then find the value of m in kg.
View SolutionA cubical block of wood of side 5 cm is placed on a table. Find the thrust by the block wood on the table, if density of wood is 5gcm−3 and g is 10 ms−2.
View SolutionA cubical block of wood of length 5 cm is kept on a table top. The density of the block is 800kg/m3 and g=9.8m/s2 . Find the pressure exerted by the wooden block on the table top.
View SolutionA cubical block of wood 10cm on a side, floats at the interface of oil and water as shown in figure. The density of oil is 0.6gcm−3 and density of water is 1gcm−3. The mass of the block is
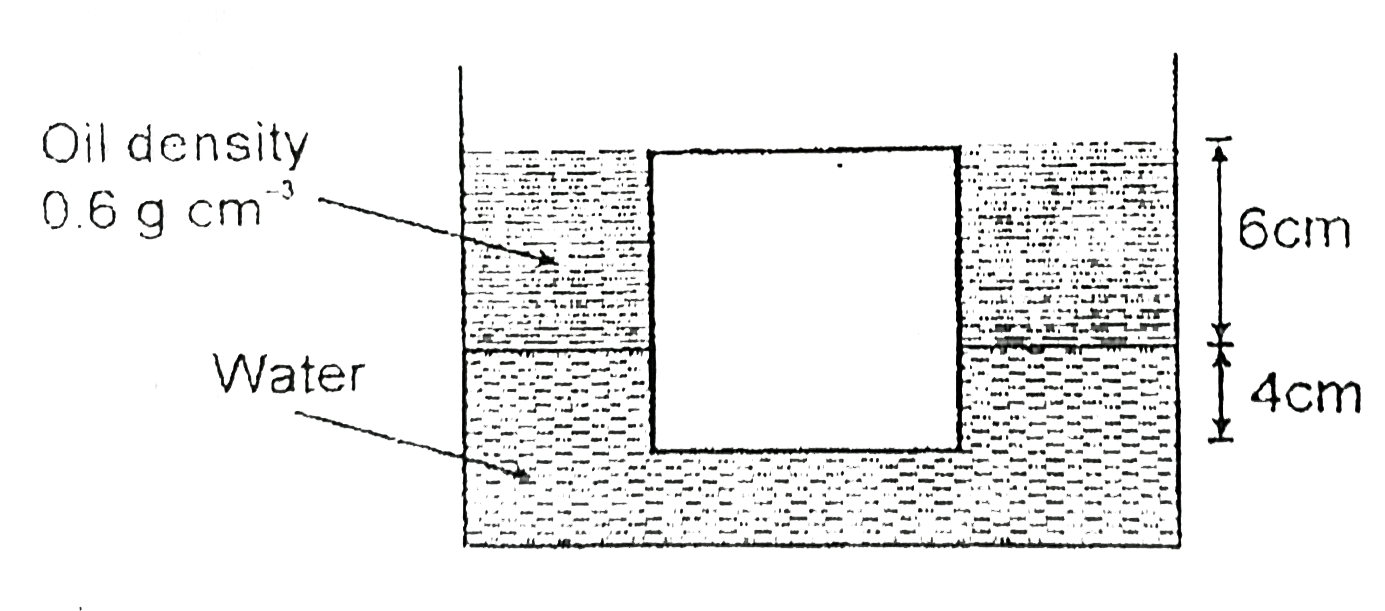
View SolutionA cubical block of wood 10cm on a side floats at the interface between oil and water, as in fig. with its lower face 2cm below the interface. The intensity of the oli is 0.6gcm−3. The mass of the block is 1kg

View Solution
