A tube of length 1 and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The velocity v of flow is given by v=v0(1−r2/R2) Where r is the distance of flowing fluid from the axis.
the volume of fluid flowing across the section. Of the tube, in unit time is 2πv0(R24)
the kinetic energy of the fluid within the volume of the tube is K.E=πρlv20(R26)
the frictional force exerted on the tube by the fluid is F=4πηkv0
the pressure difference at the ends of tube is P=4ηlv0R2
The correct Answer is:A, B, C, D
The volume of fluid flowing through this section per second dv=(2πrdr)v0(1−r2R2)
Total volume V=∫R0(2πrdr)v0(1−r2R2)
=2πv0(R24)
(ii). The kinetic energy of the fluid within the volme element of thickness dr
K.E. of fluid within the tube is
=12(2πl)ρv20∫R0(1−r2R2)rdr
we get K.Eπρlv20(R26)
(iii). The viscous drag exerts a force on the tube F=−ηA(dvdr)e=R
here (dvdr)r=R=v0(−2rR)r−R=−2v0/R
∴F=4πηlv0
(iv). ΔP=P2−P1=P
where P1=0 and P2=p
P=force(F)area(πR2)=4ηlv0R2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Comprehension Type Questions
40 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Paragraph Type Questions
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Statement Type Questions
16 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
A tube of length l and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The fluid flow velocity depends on the distance r from the axis of the tube as v=v0(1−r2/R2). Find:
(a) the volume of the fluid flowing across the section of the tube per unit time:
(b) the kinetic energy of the fluid within the tube's volume,
(c) the friction force exerted on the tube by the fluid,
(d) the pressure difference at the ends of the tube.
View SolutionThe velocity of liquid (v) in steady flow at a location through cylindrical pipe is given by v=v0(1−r2R2), where r is the radial distance of that location from the axis of the pipe and R is the inner radius of pipe. If R = 10 cm. volume rate of flow through the pipe is π/2×10−2m3s−1 and the coefficient of viscosity of the liquid is 0.75 N sm−2, find the magnitude of the viscous force per unit area, in Nm−2 at r = 4 cm.
View Solution
Knowledge Check
A tube of length 1 and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The velocity v of flow is given by v=v0(1−r2/R2) Where r is the distance of flowing fluid from the axis.
A4πηlV0B2πηlV0CπηlV0D23πηlV0Turpentine oil is flowing through a tube of length L and radius r. The pressure difference between the two ends of the tube is p , the viscosity of the coil is given by η=p(r2−x2)4vL, where v is the velocity of oil at a distance x from the axis of the tube. From this relation, the dimensions of viscosity η are
A[M0L0T0]B[MLT−1]C[ML2T−2]D[ML−1T−1]A sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
the maximum electric field intensity isAEm=ρ0R9εBEm=ρ0ε9RCE_m=(rhoR)/(3epsilon)DEm=ρ0R6ε
A cylindrical metal rod of radius "R" carries a current l .The velocity of free electrons drifting at a distance r(
View SolutionA current is flowing through a cylinderical conductor of radius R, such that current density at any cross-section is given by J=J0(1−rR), where r is radial distance from axis of the cylinder .Calculate the total current through the cross-section of the conductor.
View SolutionThe figure shows a non-viscous, incompressible and steady flow in front of a sphere. A-B is a horizontal streamline. It is known that the fluid velocity along this streamline is given by V=V0(1+R3x3).V0 is velocity of flow on this streamline when x→(−∞). It is given that pressure at x→(−∞) is P0 and density of liquid is ρ.
(i) Write the variation of pressure along the streamline from pointA, far away from the sphere, to point B on the spehre.
(ii) Plot the variation of pressure along the streamline from x=−∞ to x=-R.
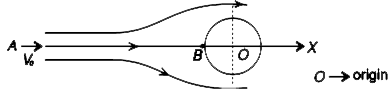
View SolutionA long cylindrical conductor of cross-sectional area A and radius a is made of material whose resistivity depends only on a distance r from the axis of conductor, given by ρ=cr2, where c is a constant. Find the resistance per unit length of the conductor and the electric field strength due to which a current I flows in it.
View SolutionAn incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:

View Solution
