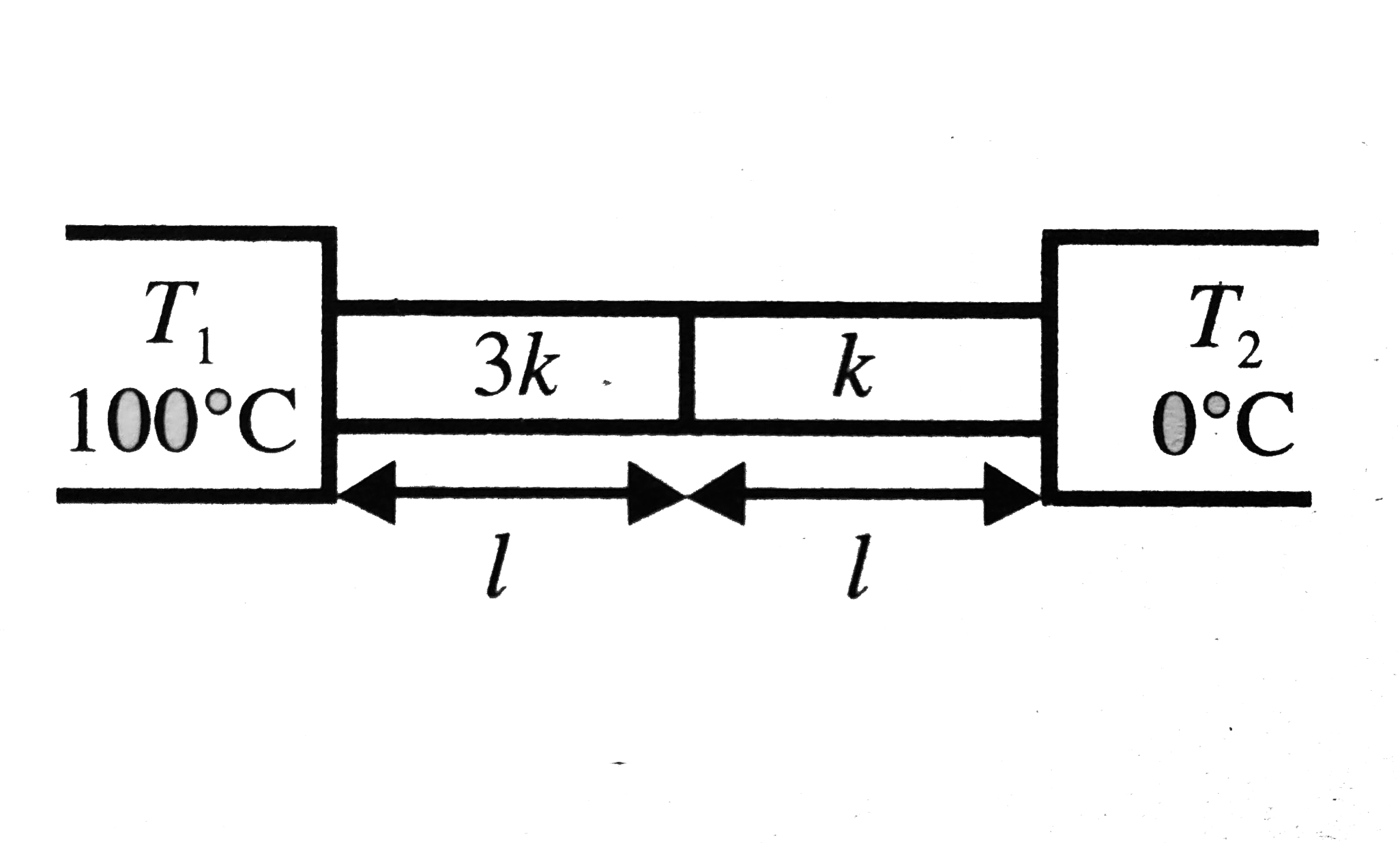
Two rods A and B of same cross sectional are A and length l connected in series between a source
(T1=100∘C) and a sink (T2=0∘C) as shown in The rod is laterally insulated

The ratio of thermal resistance of the rod is .
RARB=13
RARB=3
RARB=34
43
The correct Answer is:A
Step by step video, text & image solution for Two rods A and B of same cross sectional are A and length l connected in series between a source (T_(1) =100^(@)C) and a sink (T_(2) =0^(@)C) as shown in The rod is laterally insulated The ratio of thermal resistance of the rod is . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-I(H.W)
19 Videos
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-II(C.W)
27 Videos
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - SINGLE ANSWER QUESTIONS Passage -1
1 Video
- THERMODYNAMICSBOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise
187 Videos
- UNITS AND MEASUREMENTSBOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION
23 Videos
Similar Questions
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionTwo cylindrical rods of same cross-section area and same length are connected in series to an ideal cell as shown.The resistivity of left rod is ρ and that if right rod is 2ρ Then the variation of potential and electric field at any point P distant x from left end of combined rod system are given by
View Solution
Knowledge Check
Two rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
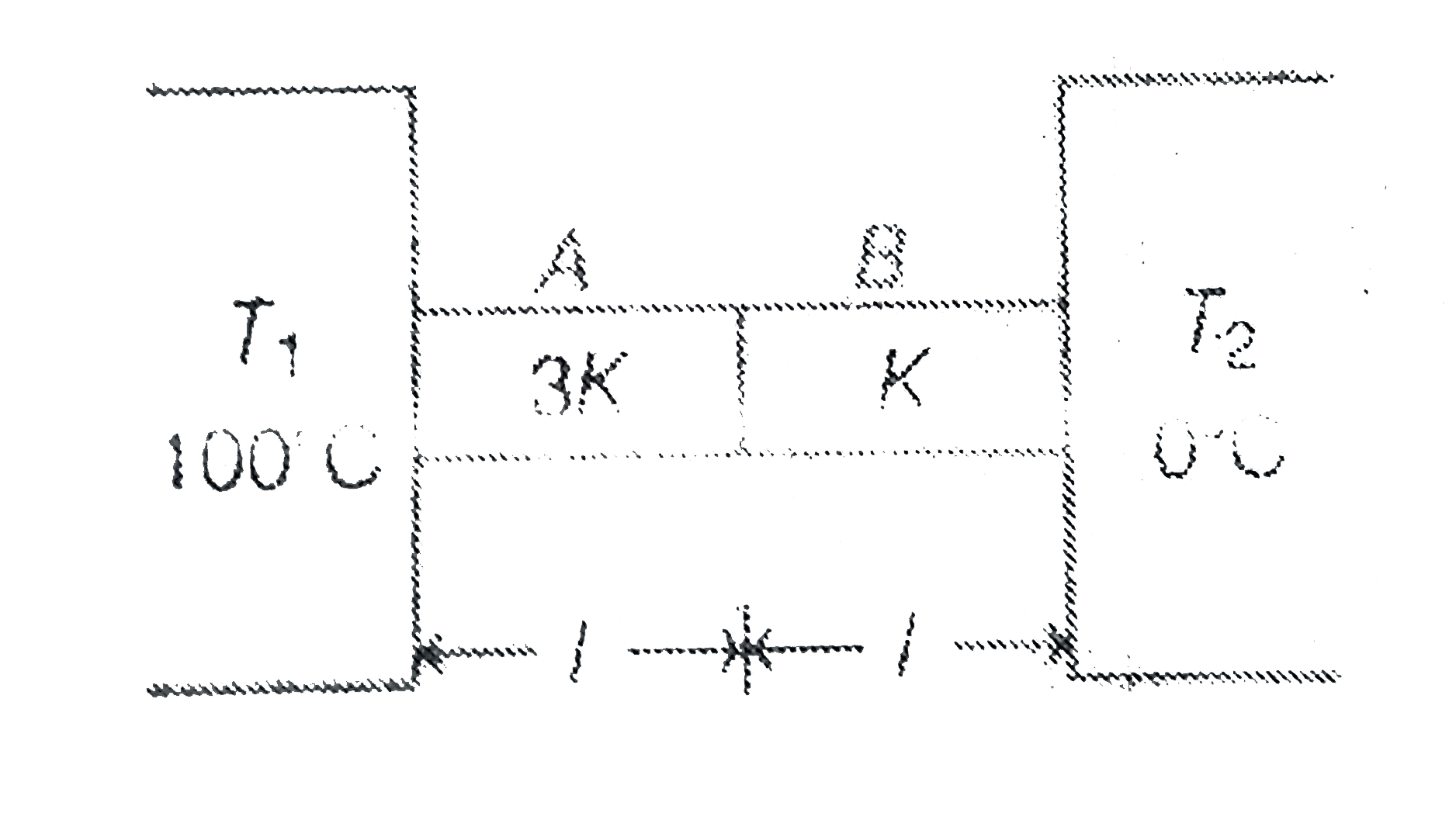
The ratio of the thermal resistance of the rods isARARB=13BRARB=3CRARB=34DRARB=43Two rods A and B of same cross sectional are A and length l connected in series between a source
(T1=100∘C) and a sink (T2=0∘C) as shown in The rod is laterally insulated

If AA and TB are the temperature drops across temperature gradients the rod A and B then .ATAAB=31BTATB=13CTATB=34DTATB=43Two rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.

If TA and TB are the temperature drops across the rod A and B, thenATATB=31BTATB=13CTATB=34DTATB=43
Two rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
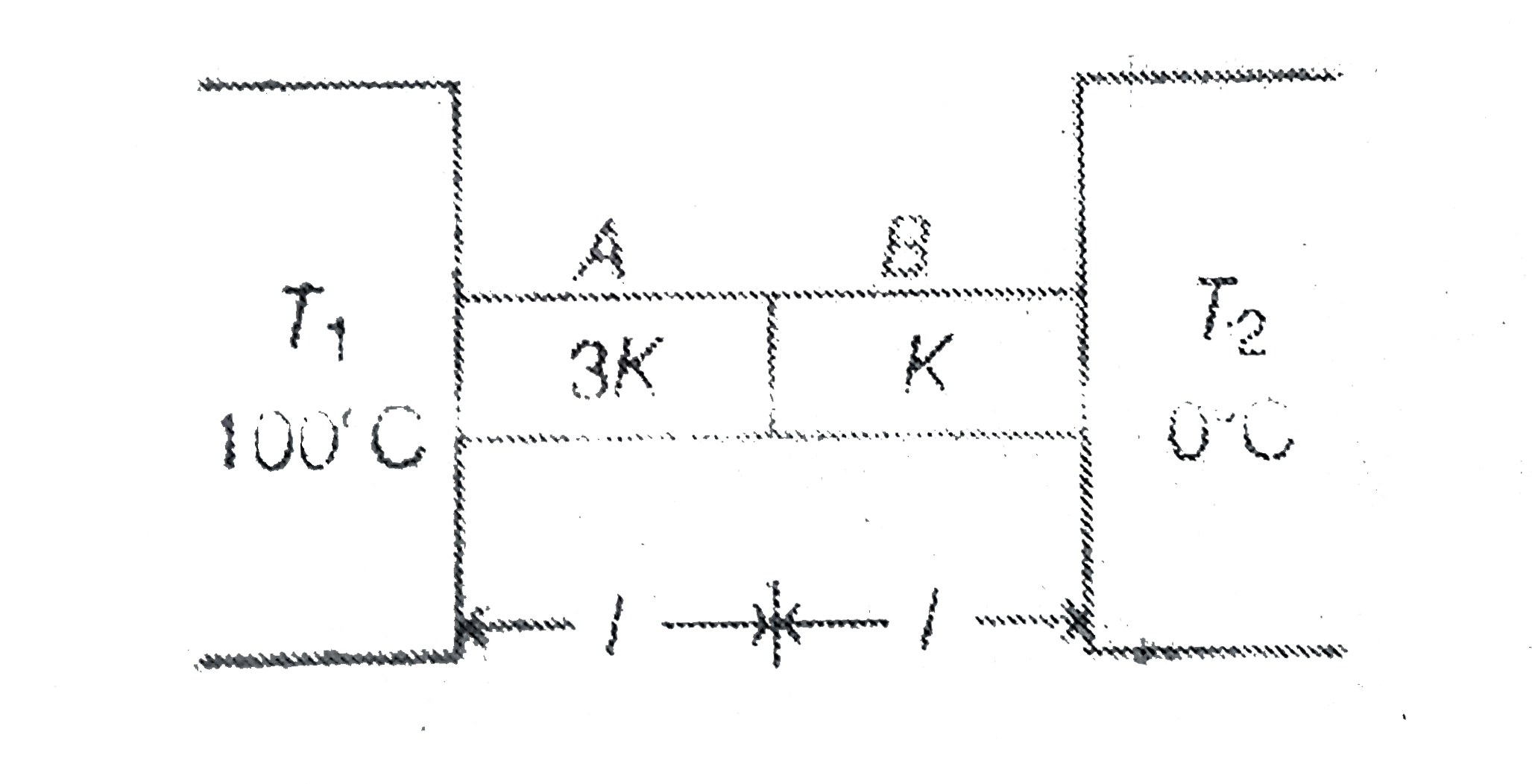
If GA and GB are the temperature gradients across the rod A and B, then
View SolutionTwo conducting rods A and B of same length and cross-sectional area are connected (i) In series (ii) In parallel as shown. In both combination a temperature difference of 100°C is maintained. If thermal conductivity of A is 3 K and that of B is K then the ratio of heat current flowing in parallel combination to that flowing in series combination is

View SolutionTwo identical rods with different thermal conductivities k1 & k2 and different temperatures are first placed along length and then along area, then the ratio of rates of heat flow in both cases is
View SolutionA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
View SolutionA rod of 1m length and area of cross-section 1cm2 is connected across two heat reservoirs at temperature 100∘C and 0∘C as shown. The heat flow per second through the rod in steady state will be [Thermal conductivity of material of rod =0.09kilocalm−1s−1('∘C)]

View Solution