Two cylinders are connected by a fixed diathermic partition A and a removable adiabatic partition B is placed adjacent to A as shown in the figure. Inititally n moles of an ideal monoatomic gas in present in both the cylinders an normal atmospheric pressure p0 . Both the gases occupy same volume V0 , initially.
Now the piston of the left cylinder is compressed in adiabatic manner so that volume of the lift portion becomes V02 and then the left piston clamped. Again the adiabatic slider B is removed so equilibrium. Assume all other surfaces except A to be adiabatic. For this situation, mark out the correct statement (s).

Just after the removal of adiabatic separator B , the pressure in the lift and right chambers are 2γp0 and p0 , respectively.
A fter the removal of adiabatic separtor B , the gas in right chamber expands under constant pressure process.
Workdone by the gas of the right chamber on surroundings during its expansion is 0.22p0V0 .
During the expansion of gas in right chamber, the energy transferred from the left chamber to right chamber is 0.55p0V0 where γ=53 .
The correct Answer is:A, B, C, D
As the gas of the left chamber is compressed adiabatically to half to its initial volume.
p0V0=p1(V0/2)γ,⇒p1=p0×2γ
i.e., pressure in the left chamber after the completion of adiabatic process is p1 while pressure in the right chamber remains same as it is isolated from surrondings or you say no energy transfer berween the right chamber and the surroundings occur. Due to this adiabatic compression, temperature will also change in the left chamber.
T0Vγ−10=T1(V0/2)γ−1,⇒T1=2γ−1T0
Where T0=p0V0nR
When adiabatic separator is removed, temperature on both sides are different, temperature on left is T1 while temperature on right is Y0 , so heat transfer takes place from left chamber to right chamber and the gas in cahmber starts expanding, as piston (right side) is free to move, the pressure remains constant as p0 , So , expansion in right chamber is taking place at constant temperature , During this expansion of gas in right chamber. the volume of gas in left chamber remains constant but temperature and pressure change, For the instant just a fter the removal of adiabatic separator we can take the pessure of gas in left chamber as the same just before the removal i.e., p0×2γ.
Let the final temperature on both the side be
T, then the energy transferred from left to right is used to incease the temperature of the tight part and to expand the gas.
i.e., nCv(T1−T)=nCp(T−T0)
=nCV(T−T0)+W
⇒T=5T0+3T18
=(5+3×2γ−18)T0≅1.22T0
So, the energy transferred is,
Q=nCV(T1−T)=3nR2(2γ−1−1.22)T0
=0.55p0V0
Work done, W=p0(Vf−Vi=nR(T−T0)
=0.22nRT0≅0.22p0V0
Topper's Solved these Questions
Similar Questions
A diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.
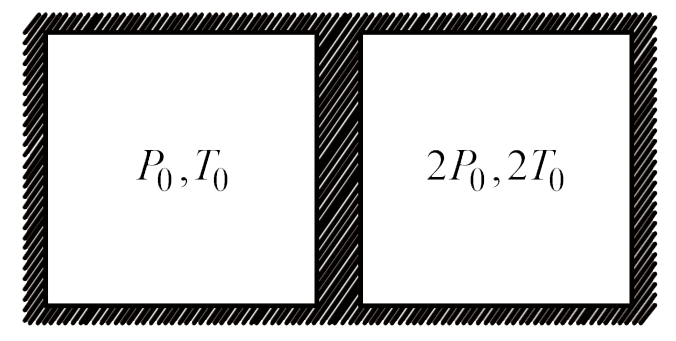
The pressure in left compartment after thermal equilibrium is achieved isView SolutionA diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.

The heat that flown from right compartment to left compartment before thermal equilibrium is achieved isView Solution
Knowledge Check
- Question 1 - Select One or More
In the arrangement shown in Fig. gas is thermally insulated. An ideal gas is filled in the cylinder having pressure P0 (gt atmospheric pressure P0). The spring of force constant K is initially unstretched. The piston of mass m and area S is frictionless. In equilibrium, the piston rises up by distance x0, then
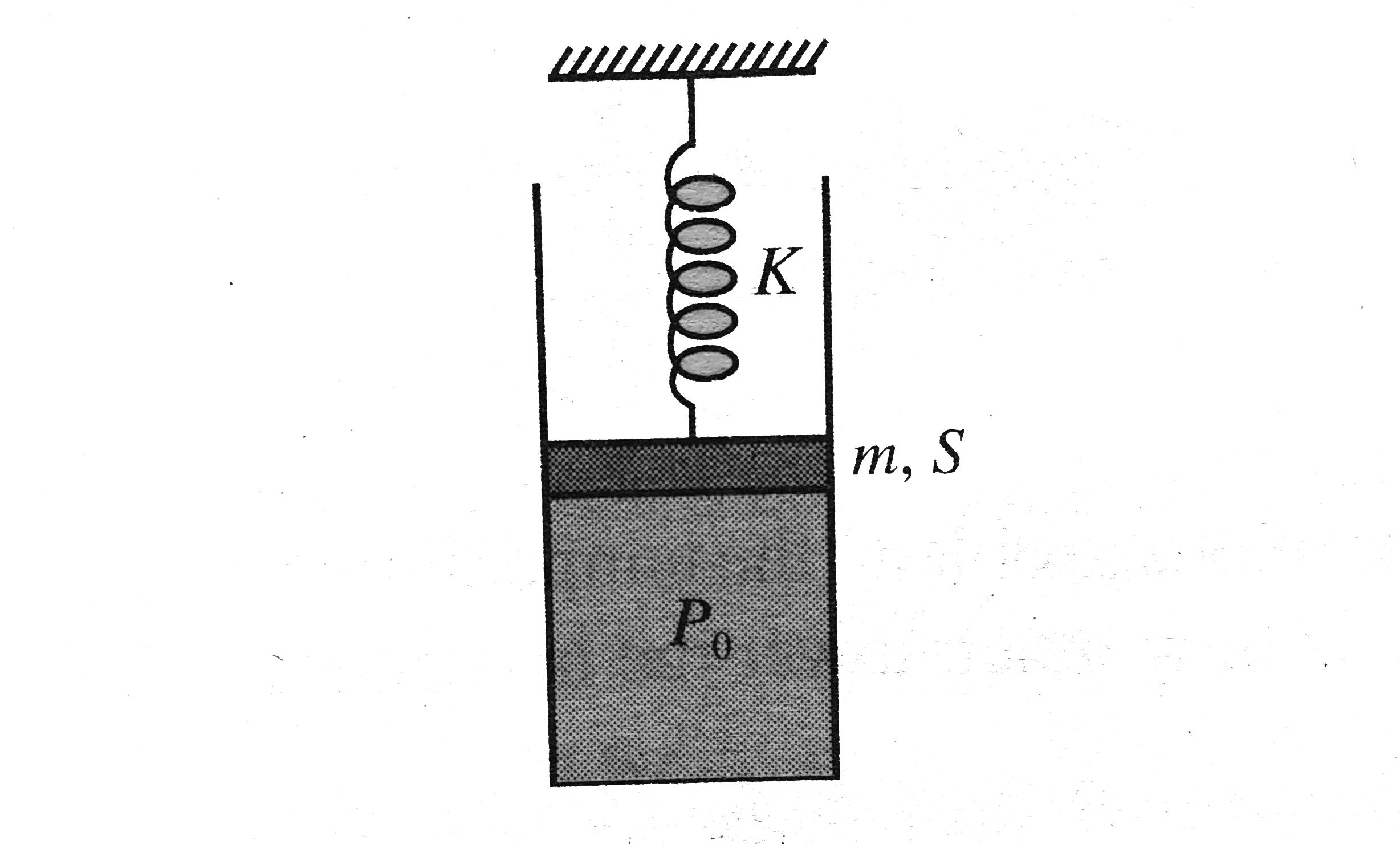 Afinal pressure of the gas is P0+Kx0S+mgSBwork done by the gas is 12Kx20+mgx0Cdecrease in internal energy of the gas is 12Kx20+mgx0+P0Sx0Dall of the above
Afinal pressure of the gas is P0+Kx0S+mgSBwork done by the gas is 12Kx20+mgx0Cdecrease in internal energy of the gas is 12Kx20+mgx0+P0Sx0Dall of the above - Question 2 - Select One
A ideal gas is kept in a cylinder of cross sectional area A and volume v0. The mass of the gas enclosed is M and bulk modulus B. If the piston of the cylinder is pressed by small x, then find the time period of small oscillations,
A2π√BA2MV0B2π√BAMV20C2π√BAMV0D2π√B2AMV0 - Question 3 - Select One
Two idential cylinders contain helium at 2.5 atmosphere and Argon at 1 atmosphere respectively. If both the gases are filled in one of the cylinders then the pressure would be
A3.5 atmospheresB1.5 atmospheresC1.75 atmospheresD1 atmosphere
A diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.

If the pin which was keeping the piston fixed is removed and the piston is allowed to slide slowly such that a state of mechanical equilibrium is achieved. The volume of left compartment when piston is in equilibrium isView SolutionTwo samples A and B of a certain gas, which are initially at the same temperature and pressure, are compressed from volume V to V /2. A is compressed isothermally, while Bis compressed adiabatically. The final pressure of A is
View SolutionIf a gas of a volume V1 at pressure p1 is compressed adiabatically to volume V2 and pressure p2, calculate the work done by the gas.
View SolutionPV Diagram for ideal gas in piston cylinder assembly undergoing a thermodynamic process is shown in figure. Process is
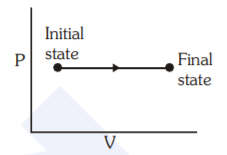 View Solution
View SolutionA monoatomic gas is compressed adiabatically to 1/4th of its original volume, the final pressure of gas in terms of initial pressure P is
View Solution

