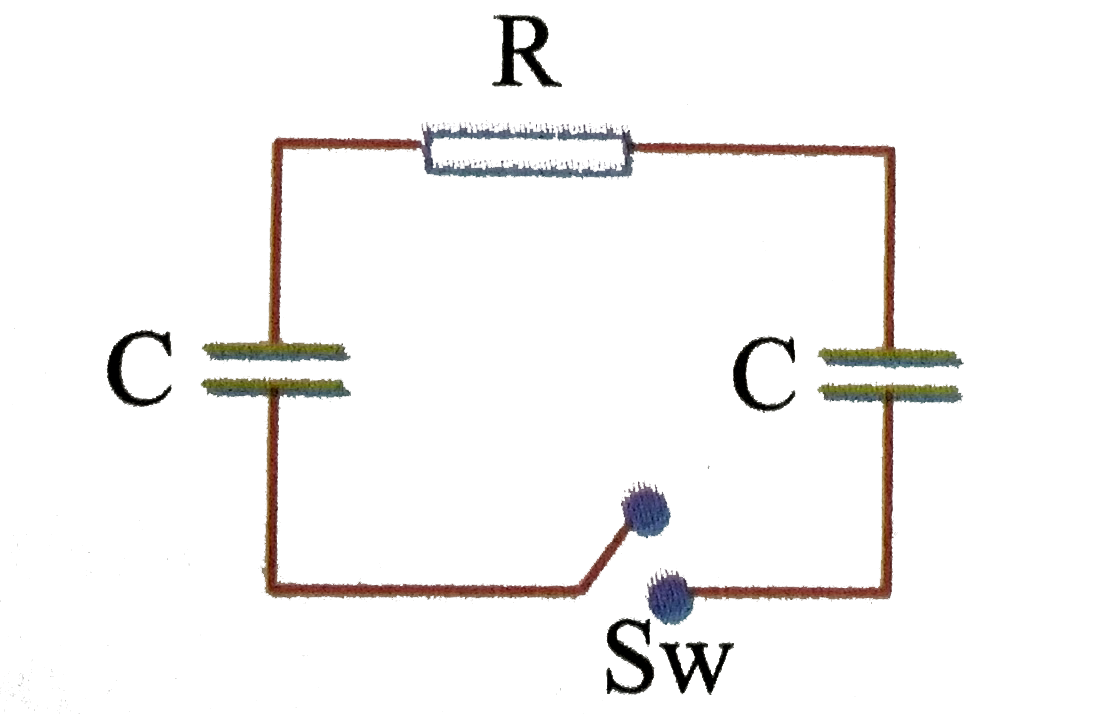
In the circuit shown, a capacitor charged to a potential difference V0 is connected to an uncharged capacitor through a resistor at t=0, by closing the switch. Find current in the circuit as function of time.
 .
.
The correct Answer is:V0Re−2t/RC.
V0Re−2t/RC
Let, at any moment of time, charge flown be q then current i=dqdt
Applying loop rule in the circuit , −Δφ=0, we get :
dqdtIR−(CV0−q)C+qC=0 or
dqCV0−2q=1RCdt
So, InCV0−2qCV0=−2tRCfor0≤t≤t
or, q=CV02(−e−2tRC)
Hence, i=dqdt=CV022RCe−2tRC=V0Re−2t/RC.
 .
.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Previous IIT-JEE16videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Level-VI28videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - ATOMS EXERCISE - EXERCISE -447videos
ATOMS
- BOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)25videos
COMMUNICATION SYSTEM
Similar Questions
A circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the circuit shown in figure-3.345 the capacitor of capacitance C is charged to a potential difference V. The current in the circuit just after the closing of switch S is :
 AV3RB3VRCV2RDzero
AV3RB3VRCV2RDzero - Question 2 - Select One or More
n the circuit shown in the figure, the capacitor C is charged to a potential Vo The heat generated and charge flow, in the circuit to when the switch S is closed, is
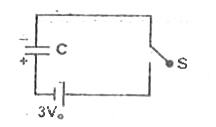 A△q=2CVoB△H=4CVoC△q=4CVoD△H=8CVo
A△q=2CVoB△H=4CVoC△q=4CVoD△H=8CVo - Question 3 - Select One or More
A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)V
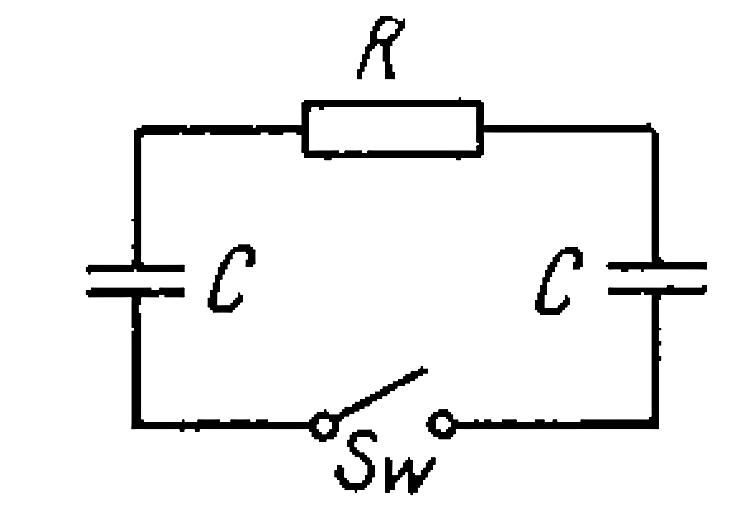
In a circuit shown in fig. the capacitance of each capacitor is equal to C and the resistance, to R One of the capacitor was connected to a voltage V0 and then at the moment t=0 was shorted by means of the swich Sw. Find:
(a) a current I in the circuit as a function of time t:
(b) the amount of generated heat provided a dependence I(t) is known.
 View Solution
View SolutionIn the circuit shown. Initially the capacitor is uncharged. The switch S is closed at time t=0. Then
 View Solution
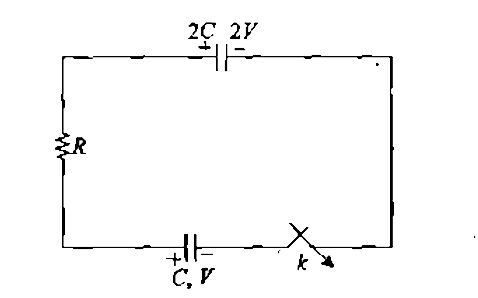
View SolutionTwo parallel plate capacitor of capacitance 2C and C are charged to the potentials 2 V and V respectively and are connected in a circuit along with a resistance R as shown in the diagram. The switch k is closed at t=0. Find the current in the circuit as a function of time and total heat produced in the circuit
 View Solution
View SolutionA circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t=0 to a source of ac voltage V=Vmcosωt . Find the current in the circuit as a function of time t.
View SolutionA capacitor is charged to a potential of V0. It is connected with an inductor through a switch S. The switch is closed at time t=0. Which of the following statement(s) is/are correct?
 View Solution
View Solution

