Let P and Q be two points on the circle |w|=r represented by w1 and w2 respectively, then the complex number representing the point of intersection of the tangents of P and Q is :
w1w22(w1+w2)
2w1¯¯¯w2w1+w2
2w1w2w1+w2
2¯¯¯w1w2w1+w2
The correct Answer is:C
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE-2 : ONE OR MORE THAN ONE ANSWER IS / ARE CORRECT
10 Videos
- COMPLEX NUMBERSBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE-3:COMPREHENSION TYPE PROBLEMS
9 Videos
- CIRCLEBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - CIRCLEEXERCISE - Exercise - 5 : Subjective Type Problems
13 Videos
- COMPOUND ANGLESBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - COMPOUND ANGLESEXERCISE - Exercise-5 : Subjective Type Problems
31 Videos
Similar Questions
Knowledge Check
Let OP.OQ=1 and let O,P and Q be three collinear points. If O and Q represent the complex numbers of origin and z respectively, then P represents
A1zB¯zC1¯zD−zIn a given parallelogram, if the points P1 and P2 represent two complex numbers z1 and z2, then the point P3 represents the number
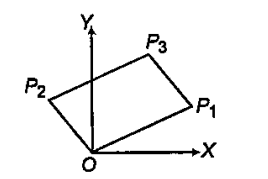 Az1+z2Bz1−z2Cz1×z2Dz1+z2
Az1+z2Bz1−z2Cz1×z2Dz1+z2P and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
A80∘B200∘C160∘D100∘
Let OP.OQ=1 and let O,P and Q be three collinear points. If O and Q represent the complex numbers of origin and z respectively, then P represents
View SolutionThe straight line x−2y+5=0 intersects the circle x2+y2=25 in points P and Q, the coordinates of the point of the intersection of tangents drawn at P and Q to the circle is
View SolutionIf the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View SolutionTwo circles intersects in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that the A,Q,B and T lie on a circle.
View SolutionIf y1,y2 are the ordinates of two points P and Q on the parabola and y3 is the ordinate of the intersection of tangents at P and Q, then
View Solution
