A particle moves from rest at a on the surface of a smooth circular cylinder. The equation relating αandβis 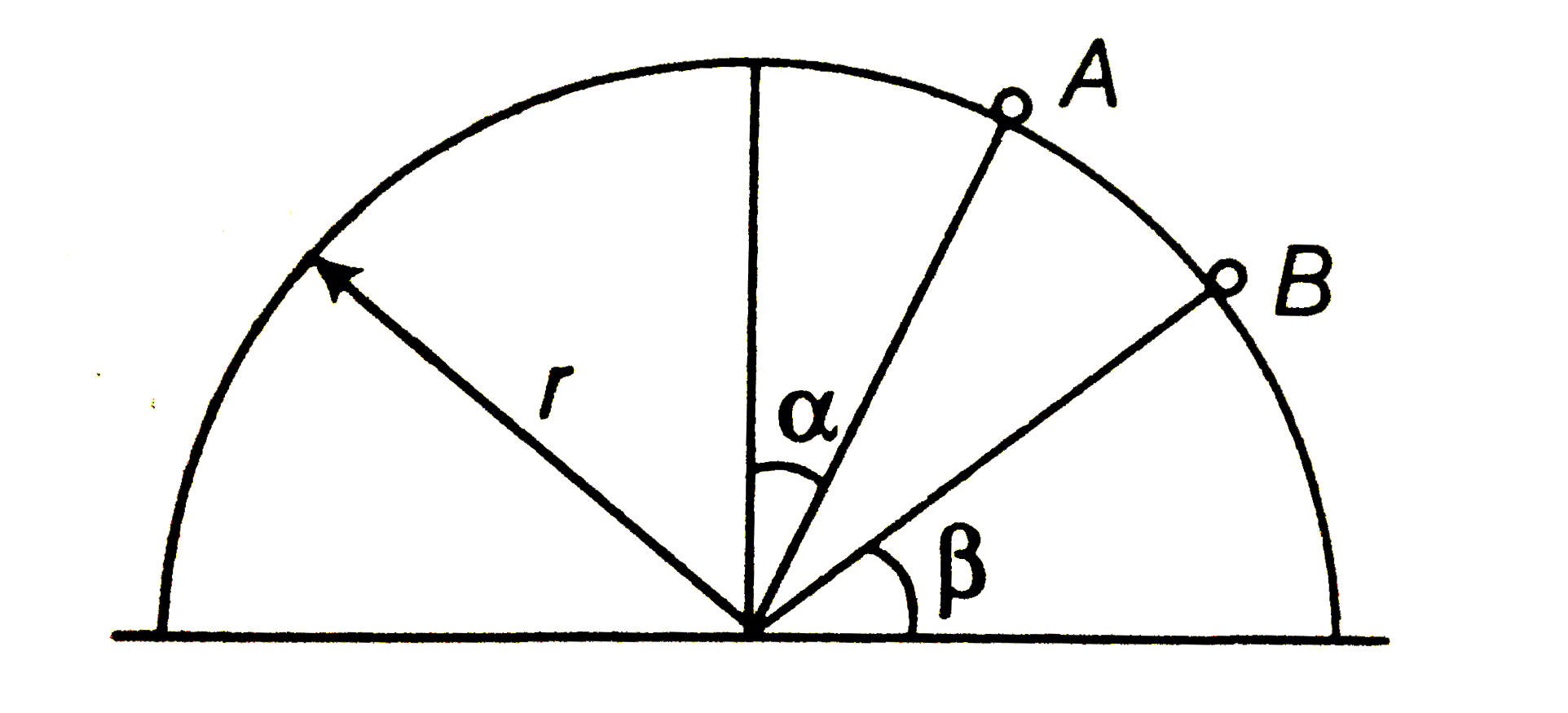
3sinα=2cosβ
3sinα=3cosβ
3sinβ=2cosα
2sinβ=3cosα
The correct Answer is:C
We have hAB =(rcosα−rsinβ)
Velocity of particle atB,
v=√2ghAB=√2g(rcosα−rsinβ)
Particle will leave contact at B if component of weight is just equal to centripetal force (towards centre).
or mgsinβ=mv2r⇒sinβ=2cosα−2sinβ
∴ 3sinβ=2cosα
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CIRCULAR MOTIONEXERCISE - MHT CET CORNER
21 Videos
- CIRCULAR MOTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE 1
54 Videos
- ATOMS, MOLECULES AND NUCLEI BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - MHT CET Corner
30 Videos
- COMMUNICATION SYSTEMBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - COMMUNICATION SYSTEMEXERCISE - MHC CET Corner
6 Videos
Similar Questions
A particle moves from rest at A on the surface of a smooth circular cylinder of radius r as shown. At B it leaves the cylinder. Find the value of 4cosα3sinβ
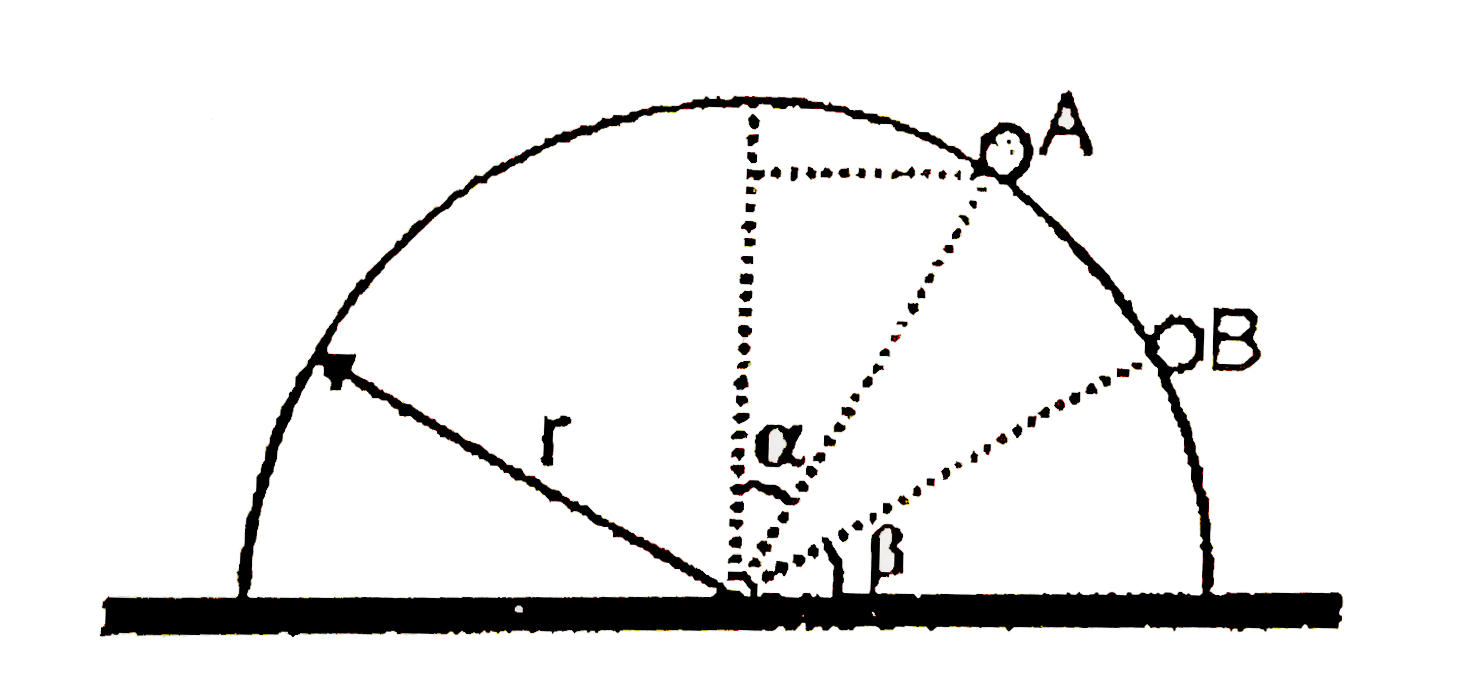
View SolutionA partical moves from rest at A on the surface of a smooth circule cylinder of radius r as shown . At B it leavels the cylinder. The equation releaseder . The equation relating αandβ is

View Solution
Knowledge Check
A practical moves from rest at A on the surface of a smooth circular cylinder of radius r as shown . At B it leaves the cylinder. The equation relating αandβ is
 A3sinα=2sinβB2sinα=3cosβC3sinβ=2cosαD2sinβ=3cosα
A3sinα=2sinβB2sinα=3cosβC3sinβ=2cosαD2sinβ=3cosαA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
AmV20Rsin2αBmV202Rcos2αC2mV20Rcos2αDmV20Rcos2αA small particle starts moving from point P along the smooth inclined surface of circular cross section seen in figure (R=5m)
 AThe different of height between the highest point of the trajectory and the point P is 6425mBThe ratio of the kinetic energies at the highest point of the trajectory and the lowest point of the circular path is 64125.CThe difference of height between the highest point of the trajectory and the point P is 3625mDThe ratio of the total mechanical energies at the highest point of the trajectory and the lowest point of the circular path is 1.
AThe different of height between the highest point of the trajectory and the point P is 6425mBThe ratio of the kinetic energies at the highest point of the trajectory and the lowest point of the circular path is 64125.CThe difference of height between the highest point of the trajectory and the point P is 3625mDThe ratio of the total mechanical energies at the highest point of the trajectory and the lowest point of the circular path is 1.
A particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0 and forms an angle α with the horizontal.
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View Solution
