Three identical spherical shells, each of mass m and radius r are placed as shown in figure. Consider an axis XX', which is touching diameter of third shell. Moment of inertia of the system consisting of these three spherical shells about XX' axis is

115mr2
mr2
165mr2
4mr2
The correct Answer is:D
The total moment of inertia of the system
l=l1+l2+l2 ….(i)
Here, l1=23mr2andl2=l3=23mr2+mr3
[From parallel axis theorem]
=53mr2
From Eq. (i),
l=23mr2+2×53mr2=mr2(23+103)=4mr2

Topper's Solved these Questions
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - MHT CET Corner
35 Videos
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - PRACTICE EXERCISE (Exercise 1 (TOPICAL PROBLEMS))
70 Videos
- REFRACTION OF LIGHTBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 2
25 Videos
- SCALARS AND VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SCALARS AND VECTORS EXERCISE - Exercise 2 (Miscellaneous Problems)
20 Videos
Similar Questions
Three idential spherical shells each of mass m and radius r are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :
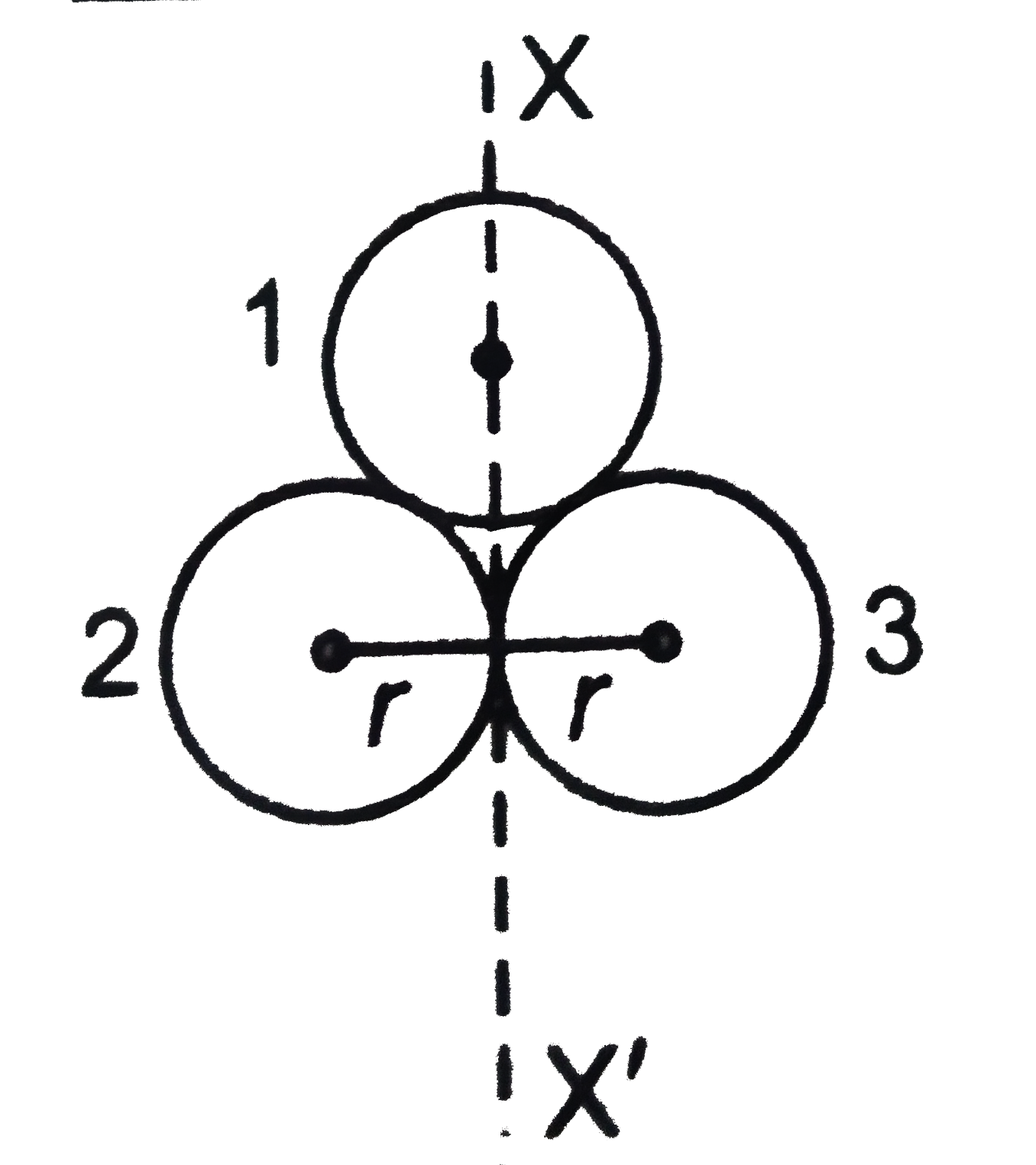
View SolutionThree idential spherical shells each of mass m and radius r are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :

View Solution
Knowledge Check
Three idential spherical shells each of mass m and radius r are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :
 A3mr2B165mr2C4mr2D115mr2
A3mr2B165mr2C4mr2D115mr2Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
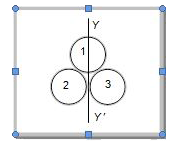 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
 A72PQ2B27PQ2C25PQ2D52PQ2
A72PQ2B27PQ2C25PQ2D52PQ2
Three identical solid discs, each of mass M and radius R, are arranged as shown in figure. The moment of inertia of the system about an axis AB will be

View SolutionThree spheres, each mass M and radius R, are arranged as shown in the figure . The moment of inertia of the system will be

View SolutionThee spheres each of mass M and radius R are placed in contact with each other as shown in the figure here. Then the moment of inertia of the system about the axis CC' is

View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be

View SolutionDerive an expression for the moment of inertia of a thin spherical shell about a diameter.
View Solution
