For a given ac $i = i_{m} sin ω t$ , show that the average power dissipated in a resistor R over complete cycle is $\frac{1}{2} i_{m}^{2} R$ .

A

$P = \frac{1}{2} i_{m}^{2} R$

B

$P = \frac{1}{4} i_{m}^{2} R$

C

$P = \frac{3}{4} i_{m}^{2} R$

D

$P = i_{m}^{2} R$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The instantaneous power dissipated in the resistor is
$P = i^{2} R = i_{m}^{2} R {sin}^{2} ω t [i = i_{m} sin ω t]$
The average value of P over a cycle is
$P_{a v} = < i^{2} R > = < i_{m}^{2} R {sin}^{2} ω t >$
Where, $P_{a v}$ denotes its average value and $< . . . >$ denotes taking average of the quantity inside the bracket. since $i_{m}^{2}$ and R are constant,
$P_{a v} = i_{m}^{2} R < {sin}^{2} ω t >$
Using the trigonometric identtify, ${sin}^{2} ω t = 1 / 2 (1 - cos 2 ω t)$ ,
we have $< {sin}^{2} ω t > = (1 / 2) (1 - < cos 2 ω t >)$ and since,
$< cos 2 ω t \geq 0$ , we have $< {sin}^{2} ω t \geq \frac{1}{2}$
thus, $P_{a v} = \frac{1}{2} i_{m}^{2} R$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

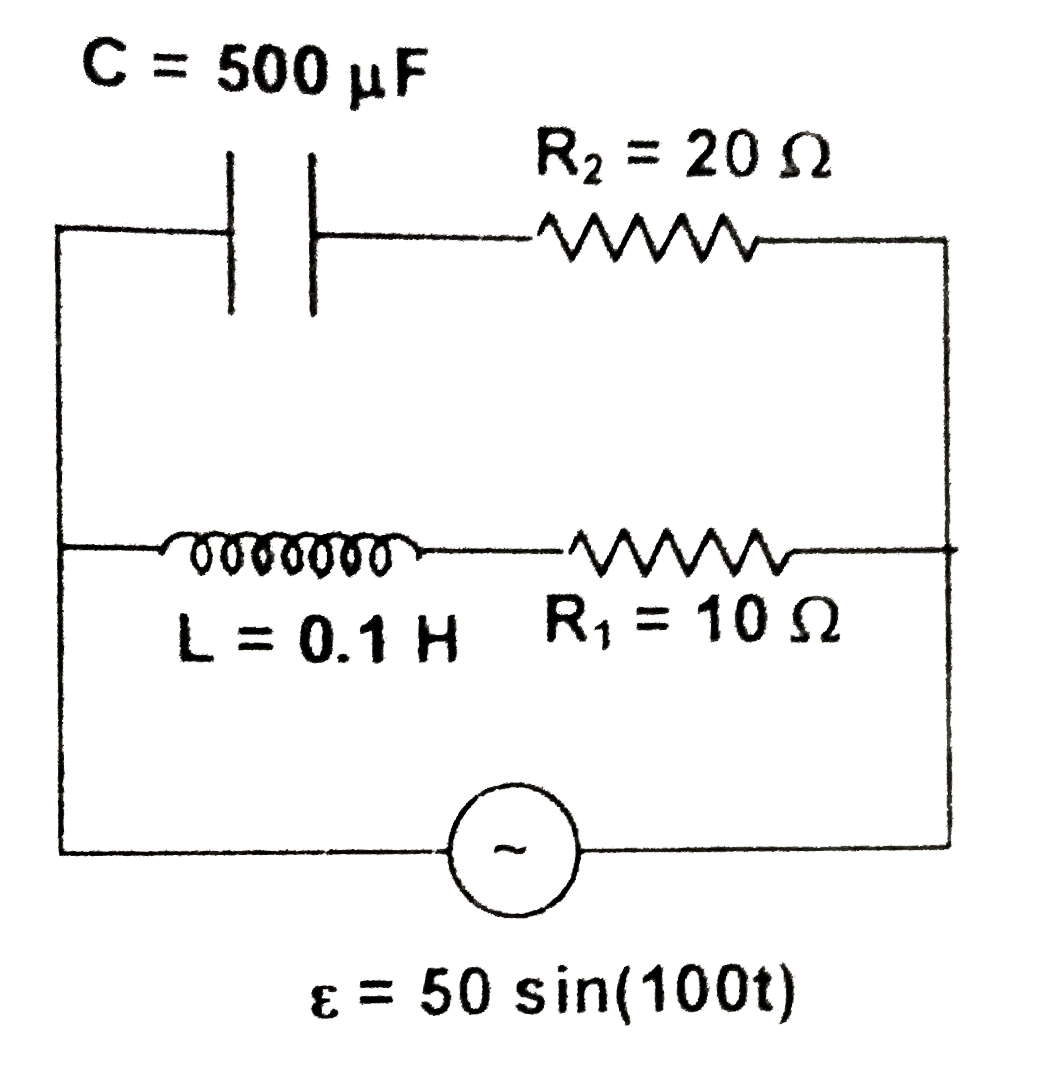
In the circuit shown the average power developed in the resistor $R_{1}$ is
A31.25 W
B62.50 W
C125 W
D250 W
Question 2 - Select One
In a series LCR circuit, an alternating emf (V) and current (I) are given by the equation $V = V_{0} sin ω t, I = I_{0} sin (ω t + \frac{π}{3})$ The average power dissipated in the circuit over a cycle of AC is
A $\frac{V_{0} I_{0}}{2}$
B $\frac{V_{0} I_{0}}{4}$
C $\frac{\sqrt{3}}{2} V_{0} I_{0}$
DZero
Question 3 - Select One
In a series L.C.R. circuit alternating emf (v) and current (i) are given by the equation $v = v_{0} sin ω t$ , $i = i_{0} sin (ω t + \frac{π}{3})$ The average power dissipated in the circuit over a cycle of AC is
A $\frac{v_{0} I_{0}}{2}$
B $\frac{v_{0} I_{0}}{4}$
C $\frac{\sqrt{3}}{2} v_{0} I_{0}$
Dzero

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-ELECTROMAGNETIC INDUCTION-Example 1

Home
Ask Doubt
Profile