In the Bohr's model of hydrogen-like atom the force between the nucleus and the electron is modified as F=e24πε0(1r2+βr3), where β is a constant. For this atom, the radius of the nth orbit in terms of the bohr radius (a0=ε0h2mπe2) is
rn=a0n−β
rn=a0n2+β
rn=a0n2−β
rn=a0n+β
The correct Answer is:B
As, force between nucleus and electron is where, r=atomic radius and e=electronic charge
From question, Fe=e24πε0(1r2+βr3), where β=constant
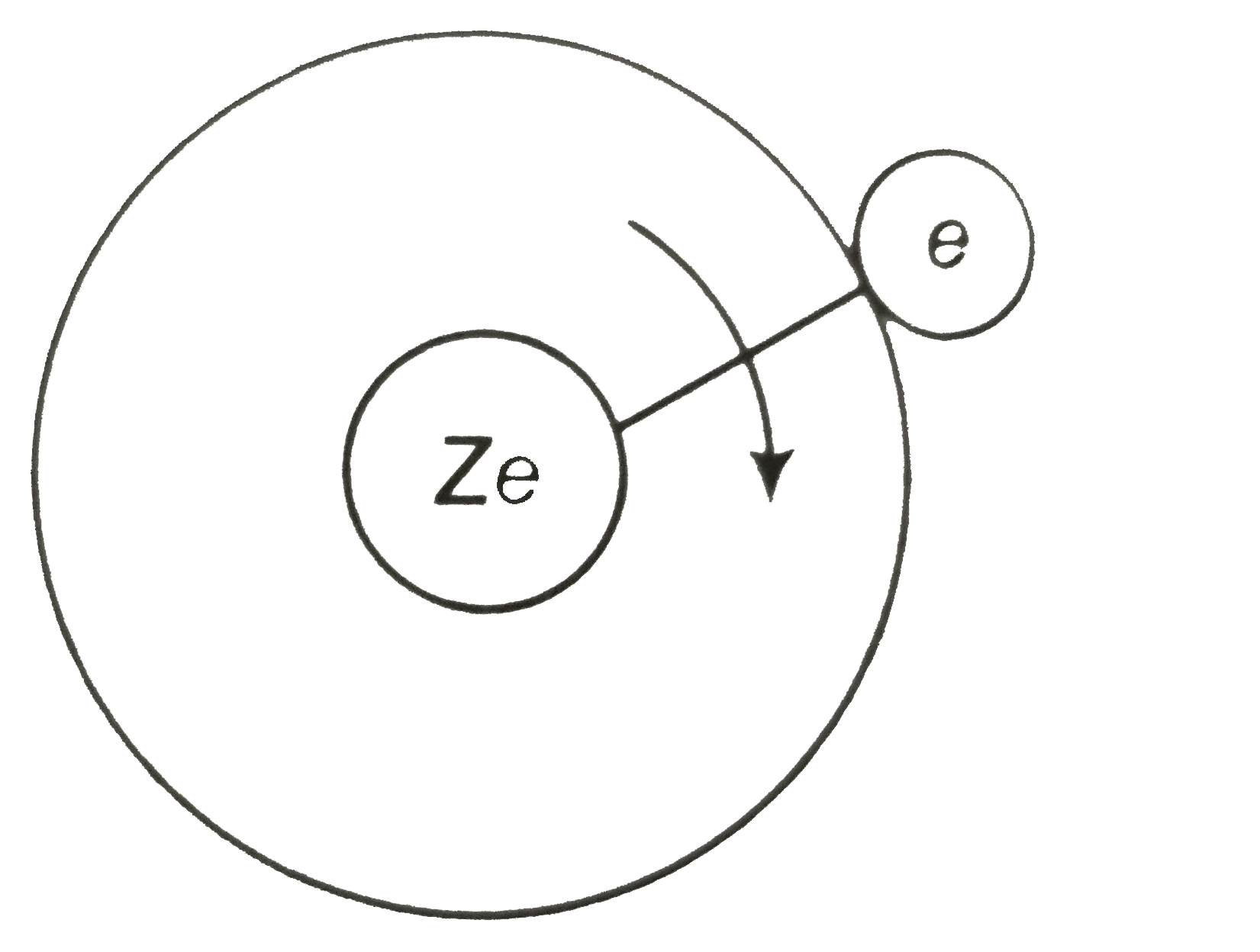
F=14πε0Ze2r2
We know that, an=rn=ε0h2n2Zmπe2
a0=r0=ε0h2Zmπe2
∴rn=ann2
As, we consider the nth electron which is attracted by nucleus while itself is repelled by the electron of inner shell to the consider shell.
Topper's Solved these Questions
- ATOMS, MOLECULES AND NUCLEI BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - MHT CET Corner
30 Videos
- ATOMS, MOLECULES AND NUCLEI BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - Exercise 1 (TOPICAL PROBLEMS)
126 Videos
- CIRCULAR MOTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CIRCULAR MOTIONEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
In the Bohr's model of hydrogen-like atom the force between the nucleus and the electron is modified as F=e24πε0(1r2+βr3), where B is a constant. For this atom, the radius of the nth orbit in terms of the Bohr radius (a0=ε0h2mπe2) is :
Arn=a0n−βBrn=a0n2+βCrn=a0n2−βDrn=a0n+βThe radius of 2nd Bohr.s orbit of hydrogen atom is :
A0.053 nmB0.106 nmC0.2116 nmD0.4256 nmThe radius of 2nd Bohr orbit of hydrogen atom is :
A0.053 nmB0.106 nmC0.2116 nmD0.4256 nm
In Bohr's mode, the atomic radius of the first orbit is r0 then the radius of the third orbit is
View SolutionIn Bohr's model, if the atomic radius of the first orbit is r0, then the radius of the fourth orbit is
View SolutionIn Bohr.s model of hydrogen atom, radius of the first orbit of an electron is r0. Then, radius of the third orbit is:
View SolutionTo calculate the size of a hydrogen anion using the Bohr model, we assume that its two electrons move in an orbit such that they are always on diametrically opposite sides of the nucleus. With each electron having the angular momentum h=h/2π, and taking electron interaction into account the radius of the orbit in terms of the Bohr radius of hydrogen atom aB=4πε0h2me2 is
View SolutionIn terms of Bohr radius a0, the radius of the second Bohr orbit of a hydrogen atom is given by
View Solution
