M and N are the mid-points of the diagonals AC and BD respectively of quadrilateral ABCD, then AB+AD+CB+CD is equal to
2 MN
2NM
4 MN
4 NM
The correct Answer is:C
Let the position vectors of A,B,C,D, M and N are
a,b,c,d, m and n.
Since, M and N are the mid-points of AC and BD.
∴m=a+c2,n=b+d2
Now, AB+AD+CD+CD
=(b−a)+(d−a)+(b−c)+(d−c)
=2(b+d)−2)a+c)
=2×2n−2×2m
=4(n−m)=4NM
Topper's Solved these Questions
- VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - VECTORS EXERCISE - (VECTORS ) Exercise 2 ( Topical problems )
88 Videos
- TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLESEXERCISE - Exercise 2 (MISCELLANEOUS PROBLEMS)
20 Videos
Similar Questions
Knowledge Check
M and N are mid-point of the diagnols AC and BD respectivley of quadrilateral ABCD, then¯¯¯¯¯¯AB+¯¯¯¯¯¯AD+¯¯¯¯¯¯CB+¯¯¯¯¯¯CD=
A2¯¯¯¯¯¯¯¯MNB2¯¯¯¯¯¯¯¯NMC4¯¯¯¯¯¯¯¯MND4¯¯¯¯¯¯¯¯NMIn trapezium ABCD,AB∣∣CDwith AB=24cm.andCD=16cm. P and Q are mid-points of the diagonals AC and BD respectively. Find the length of PQ.
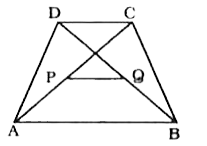 A4 cmB5 cmC8 cmD6 cm
A4 cmB5 cmC8 cmD6 cm
If PQ are the mid points of diagonal AC and BD respectively of a quadrilateral ABCD, then prove that −−→AB+−−→AD+−−→CB+−−→CD = 4 −−→PQ
View SolutionLet M,N, P and Q be the mid points of the edges AB, CD, AC and BD respectively of the tetrahedron ABCD. Further, MN is perpendicular to both AB and CD and PQ is perpendicular to both AC and BD. Then which of the following is/are correct:
View SolutionLet M,N, P and Q be the mid points of the edges AB, CD, AC and BD respectively of the tetrahedron ABCD. Further, MN is perpendicular to both AB and CD and PQ is perpendicular to both AC and BD. Then which of the following is/are correct:
View SolutionLet M,N, P and Q be the mid points of the edges AB, CD, AC and BD respectively of the tetrahedron ABCD. Further, MN is perpendicular to both AB and CD and PQ is perpendicular to both AC and BD. Then which of the following is/are correct:
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View Solution
