If u1 and u2 are the units selected in two systems of measurement and n1 and n2 their numerical values, then
n1u1=n2u2
n1u1+n2u2=0
n1n2=u1u2
(n1+u3)=(n2+u2)
The correct Answer is:a
Step by step video, text & image solution for If u_(1) and u_(2) are the units selected in two systems of measurement and n_(1) and n_(2) their numerical values, then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - MEASUREMENTSEXERCISE - CRITICAL THINKING ( SYSTEM OF UNITS)1videos
MEASUREMENTS
- BOOK - TARGET PUBLICATIONCHAPTER - MEASUREMENTSEXERCISE - CRITICAL THINKING ( FUNDAMENTAL AND DERIVED UNITS)9videos
MEASUREMENTS
- BOOK - TARGET PUBLICATIONCHAPTER - MEASUREMENTSEXERCISE - CLASSICAL THINKING( MISCELLANEOUS)1videos
MEASUREMENTS
- BOOK - TARGET PUBLICATIONCHAPTER - MAGNETISMEXERCISE - MCQs150videos
MAGNETISM
- BOOK - TARGET PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - EVALUATION TEST14videos
RAY OPTICS
Similar Questions
If u1,u2 and v1,v2 are the initial and final velocities of two particles before and after collision respectively, then v2−v1u1−u2 is called ___________.
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
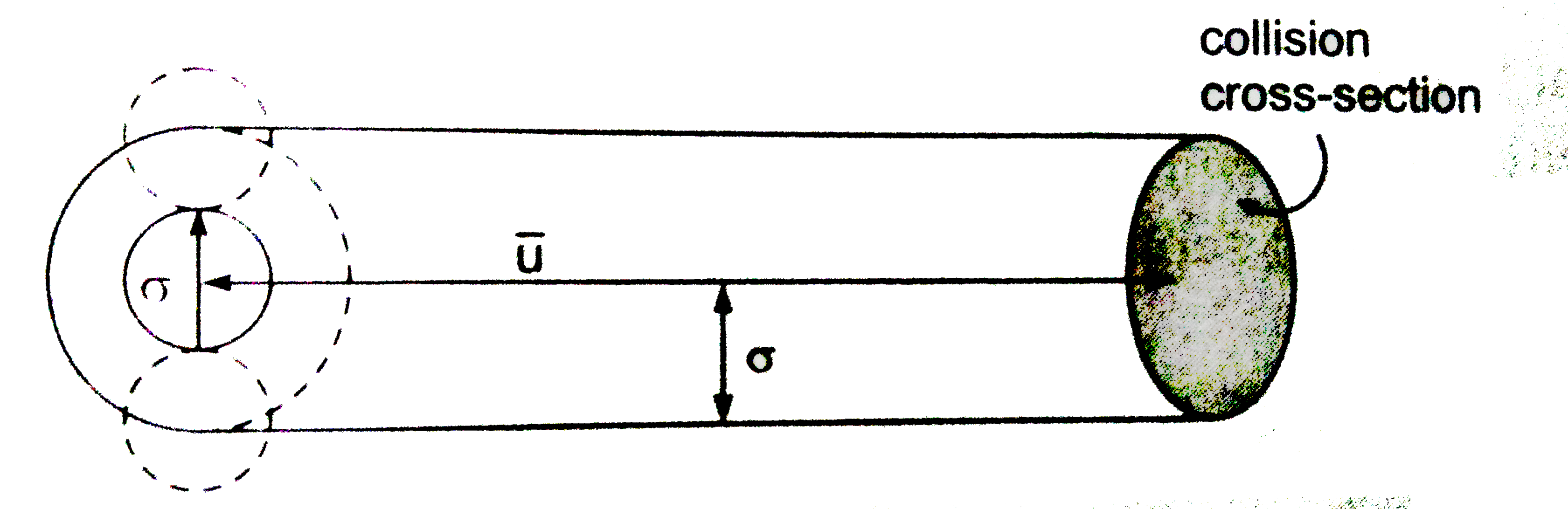
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.
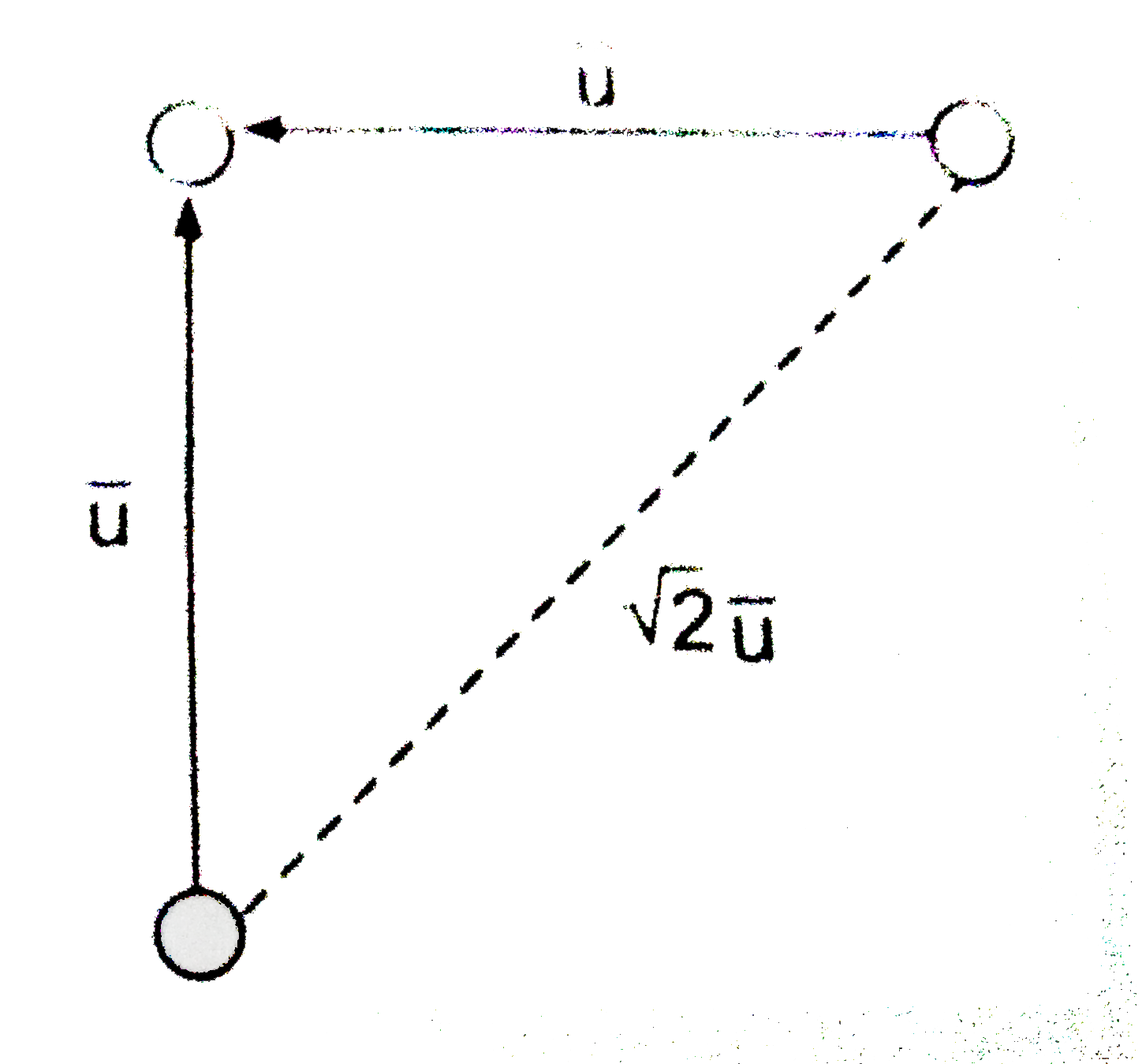
Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯2N∗
The→talνmberofbimo≤ca––rcollisionsZ_(1)perunitvolumeperunittimeisgivenby<br>Z_(1)=(1)/(2)(Z_(1)N^(**))or Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2)<br>Ifthecollsion∈volvetwounlikemo≤ce–sthentheνmberofcollisionsZ_(12)perunitvolumeperunittimeisgivenas<br>Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2)<br>whereN_(1)andN_(2)aretheνmberofmo≤ce–sperunitvolumeofthetwotypesofmo≤ce–s,sigma_(12)istheavera≥diameterofthetwomo≤ce–sandmuisthereducedmass.Themeaneepathistheavera≥distancetravel≤dbyamo≤ce–betweentwo≻essivecollisions.Wecanexpressitasfollows:<br>lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1))<br>or" "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**))<br>Threealgassamp≤s∈separateequalvolumeconta∈ersaretakenandfollow∈gdataisgiven:<br> PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate number of collision by one molecule per sec (Z1).View Solution
Knowledge Check
- Question 1 - Select One
If u1andu2 are the selected in two system of measurement and n1andn2 their nomerical values, then
An1u1=n2u2Bn1u1+n2u2=0Cn1n2=u1u2D(n1+u1)=(n2+u2) - Question 2 - Select One
Collision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
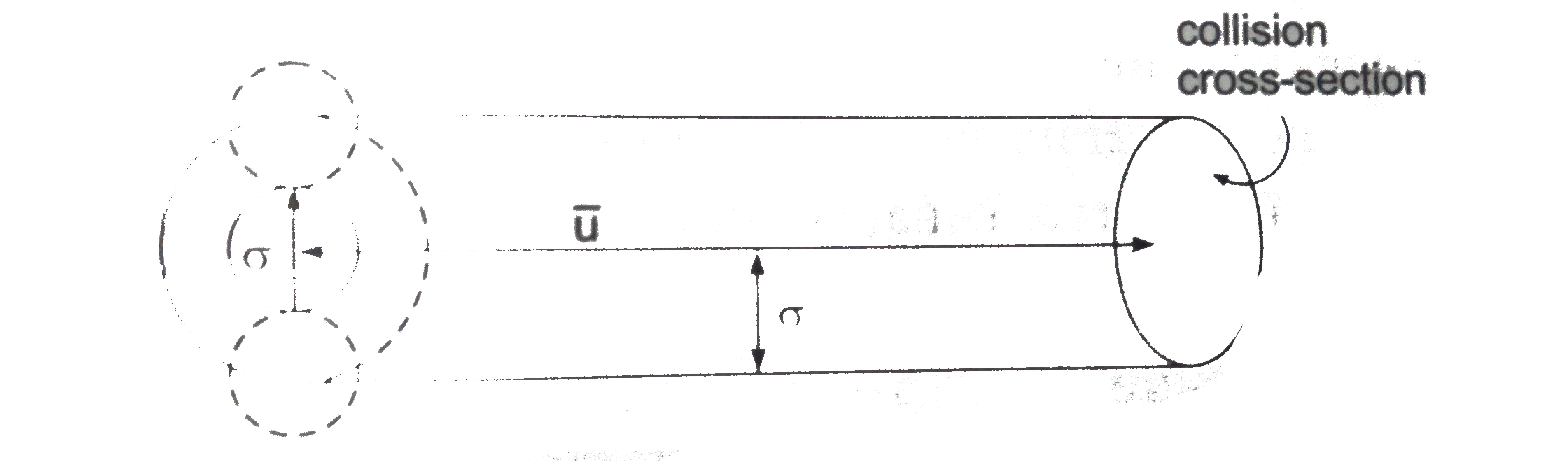
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :Aindependent to temperatureBdecreases with rise in temperatureCincreases with rise in temperatureDdirectly proportional to T2 - Question 3 - Select One
Collision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is

V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate number of collision by one molecule per sec (Z1).A4:1:4B1:4:4C4:3:2D1:2:4
When some object is kept at a distances u1andu2 from the concave mirror then size of images are found to be same. If magnitude of focal length can be written as (u1+u2)/n, then what will be the value of n ?
|0123456789|View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
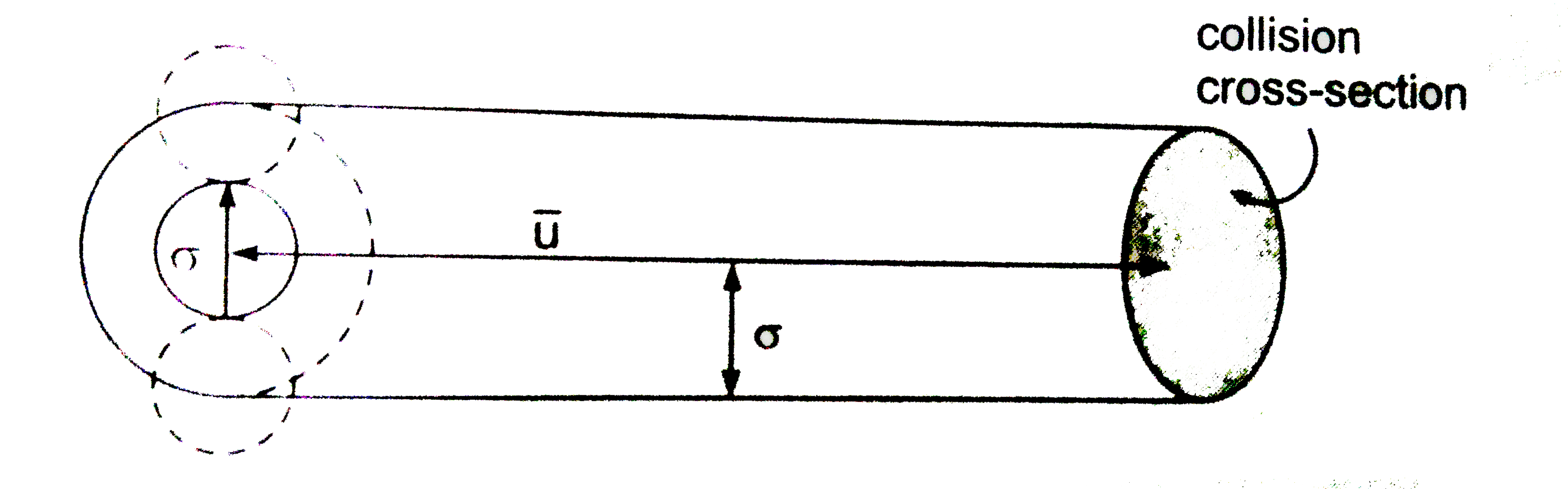
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate ratio of collision frequencies (Z11)(A:B:C) of following for the three gases.View SolutionThe numerical values and units of a physical quantity in two different system of units are n1,n2andu1,u2 respectively. Then
View SolutionThe first factor length f1 for refraction at a spherical surface is defined as the value of u corresponding to v=∞ (as shown) with refractive indices of two mediums, as n1 and n2. The second focal length f2 is defined as value of v for u=∞.
 View Solution
View SolutionP(Ui)=1n, and one urn is selected at random, then P(W) is:
View Solution

