A particle of mass m is rotated in a vertical circle by means of a string . The differnce in the tensions in the string at the bottom and the top of the circle would be

A

2 mg

B

3 mg

C

4mg

D

6 mg

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

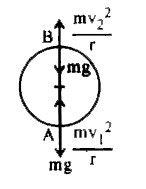
when the body is at A , there is maximum tension in the string .
$T_{max} = \frac{m v_{1}^{2}}{r} + m g$ and when it is at B , the tension in the string is minimum
and $T_{min} = \frac{m v_{2}^{2}}{r} - m g$
$∴ T_{max} - T_{min} - \frac{m}{r} (v_{1}^{2} - v_{2}^{2}) + m g - (- m g)$
But for completing the vertical circle
$V_{1} - \sqrt{5 g r} and v_{2} = \sqrt{g r}$
$∴ \frac{m}{r} (v_{1}^{2} - v_{2}^{2}) = \frac{m}{r} [5 g r - g r] = 4 m g$
$∴ T_{max} - T_{min} = 4 m g + 2 m g = 6 m g$

|

Updated on:21/07/2023

Class 12 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass m is rotating by means of a string in a vertical circle. The difference in the tension at the bottom and top would be-
A6 mg
B4 mg
C3 mg
D2 mg
Question 2 - Select One
A paricle of mass 2 kg is rotating by means of a string in a verticle circle. The difference in the tensions at the bottom and the top would be
A12 kg wt
B2 kg wt
C $>$ 12 kg wt
D $<$ 12 kg wt
Question 3 - Select One
A body of mass 0.4 kg is whirled in a vertical circle making 2 rev/sec . If the radius of the circle is 2 m , then tension in the string when the body is at the top of the circle, is
A $41.56 N$
B $89.86 N$
C $109.86 N$
D $122.2 N$

MARVEL PUBLICATION-CIRCULAR MOTION-TEST YOUR GRASP-20

Home
Ask Doubt
Profile