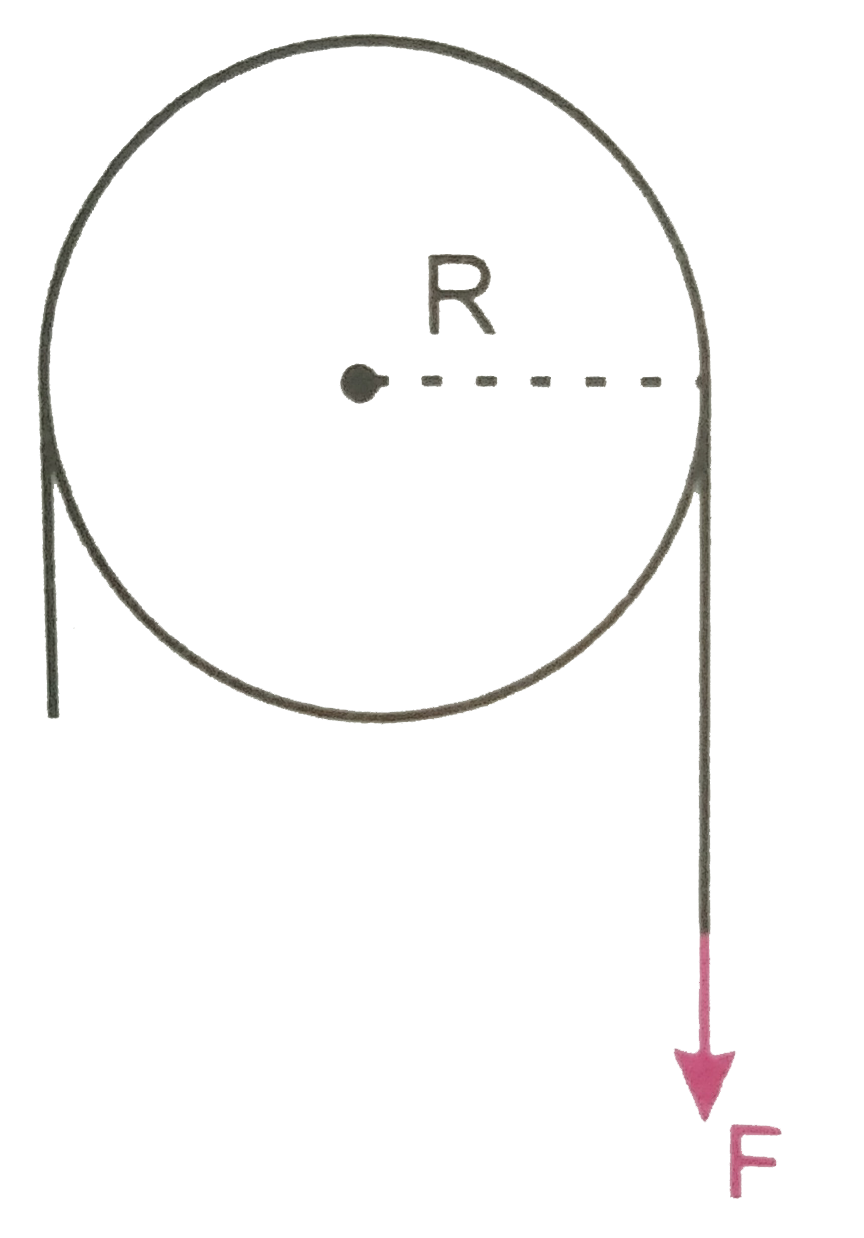
चित्र में 20 किग्रा द्रव्यमान तथा 20 सेमी त्रिज्या के गतिपालक पहिये की परिधि पर नगण्य द्रव्यमान वाली एक डोरी लपेटी गयी है। डोरी पर 25 न्यूटन का एक बल लगाया जाता है। गतिपालक पहिया एक घर्षण रहित क्षैतिज धुरी पर लगा है। गणना कीजिए : (i) पहिये का कोणीय त्वरण, (ii) डोरी के 2 मीटर खुलने तक बल द्वारा किया गया कार्य, (iii) डोरी के 2 मीटर खुलने पर पहिये की गतिज ऊर्जा।
प्रश्नानुसार, M = 20 किग्रा, R = 20 सेमी = 0.2 मीटर, F = 25 न्यूटन।
(i) पहिये का अपनी ज्यामितीय अक्ष के परितः जड़त्व आघूर्ण I==12MR2
=12×20×(0.2)2=0.4किग्रा मीटर2
पहिये पर आरोपित बल आघूर्ण τ=FR=25×0.2=5 न्यूटन मीटर
चूँकि τ=Iα
पहिये का कोणीय त्वरण α=τI=50.4=12.5रेडियन/सेकण्ड2
(ii) डोरी के 2 मीटर तक खुलने में बल द्वारा किया गया कार्य = बल x विस्थापन =25×2=50 जूल।
(iii) यदि पहिया विरामावस्था से प्रारम्भ करता है तो डोरी के 2 मीटर तक खुलने में पहिए का कोणीय विस्थापन
θ=डोरी की लम्बाईपहिए की त्रिज्या=20.2=10 रेडियन
यदि पहिये द्वारा प्राप्त कोणीय वेग ω है, तो समीकरण ω2=ω20+2αθ से,
ω2=0+2×12.5×10=250याω=√250=15.81 रेडियन/सेकण्ड।
तब पहिये की गतिज ऊर्जा E=12Iω2
= 1/2 xx 0.4 xx 250 = 50 जूल।
स्पष्ट है कि पहिये द्वारा प्राप्त गतिज ऊर्जा = बल द्वारा किया गया कार्य, क्योंकि यहाँ घर्षण नगण्य है।
Topper's Solved these Questions
- कणो का निकाय एवं घूर्णी गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - कणो का निकाय एवं घूर्णी गति EXERCISE - तथ्यात्मक प्रश्न
10 Videos
- कणो का निकाय एवं घूर्णी गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - कणो का निकाय एवं घूर्णी गति EXERCISE - सही विकल्प चुनिए
13 Videos
- उष्मागतिकीBOOK - SHIVLAAL PUBLICATIONCHAPTER - उष्मागतिकीEXERCISE - वस्तुनिष्ठ प्रश्न
164 Videos
- कणों के निकाय एवं घूर्णी गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - कणों के निकाय एवं घूर्णी गति EXERCISE - आंकिक प्रश्न
6 Videos
Similar Questions
घूर्णन गति में कौन-सी राशियाँ रैखिक गति में बल तथा द्रव्यमान के समतुल्य हैं ?
View Solutionघूर्णन गतिज ऊर्जा का विमीय सूत्र :
View Solutionतापीय साम्यावस्था में
View Solution2 किग्रा. तथा 1 किग्रा द्रव्यमानों के दो पिण्ड X-Y तल में क्रमशः बिंदुओं ( -1, 2) तथा (3, 4) पर स्थित हैं। निकाय के द्रव्यमान-केंद्र कि स्थिति ज्ञात कीजिए।
View Solutionएक इलेक्ट्रॉन (द्रव्यमान किग्रा) व एक प्रोटॉन (द्रव्यमान किग्रा) के बीच गुरुत्वाकर्षण-बल व स्थिरवैघुत बल का अनुपात ज्ञात कीजिए। (e=1.6×10−19 कूलाम तथा G=6.67×10−11 (न्यूटन-मीटर^(2)/किग्रा^(2))
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionघर्षण बल के द्वारा किया गया कार्य
View Solutionगतिज घर्षण बल के द्वारा किया गया कार्य
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View SolutionA wheel covers a distance of 1,100 cm in one round. The radius of the wheel is:
एक पहिया एक चक्कर में 1,100 सेमी की दूरी तय करता है | इस पहिये का व्यास कितना है ?
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
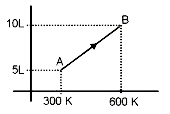
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solutionआण्विक द्रव्यमान 390 वाले एक यौगिक को प्राप्त करने के लिए आण्विक द्रव्यमान 180 वाले एक यौगिक को CH_(3)COCl के साथ ऐसिलीकृत किया जाता है। पूर्व यौगिक के प्रति अणु पर उपस्थित ऐमीनो समूहों की संख्या है:
View Solution
