A block of mass 2kg is given velocity 10m/s on a rough horizontal surface of friction coefficentμ=0.2. Find the magnitude and the direction of friction force acting on it. After how much time and at what distance it will stop ?
To solve the problem, we will break it down into several steps:
Step 1: Identify the Given Data
- Mass of the block, m=2kg
- Initial velocity, u=10m/s
- Coefficient of friction, μ=0.2
Step 2: Calculate the Normal Force
The normal force N acting on the block is equal to the weight of the block since it is on a horizontal surface.
N=mg
Where g (acceleration due to gravity) is approximately 10m/s2.
N=2kg×10m/s2=20N
Step 3: Calculate the Frictional Force
The frictional force f can be calculated using the formula:
f=μN
Substituting the values:
f=0.2×20N=4N
Step 4: Determine the Direction of the Frictional Force
Since the block is moving to the right (in the direction of the initial velocity), the frictional force will act in the opposite direction (to the left) to oppose the motion.
Step 5: Calculate the Retardation (Deceleration)
Using Newton's second law, the retardation a can be calculated as:
a=fm
Substituting the values:
a=4N2kg=2m/s2
Step 6: Calculate the Time to Stop
Using the equation of motion:
v=u−at
Where v (final velocity) is 0 when the block stops. Rearranging gives:
0=10m/s−(2m/s2)t
Solving for t:
t=10m/s2m/s2=5s
Step 7: Calculate the Distance Traveled Before Stopping
Using another equation of motion:
s=ut−12at2
Substituting the known values:
s=(10m/s)(5s)−12(2m/s2)(5s)2
Calculating:
s=50m−12×2×25=50m−25m=25m
Final Results
- Magnitude of Friction Force: 4N
- Direction of Friction Force: Left (opposite to the direction of motion)
- Time to Stop: 5s
- Distance Traveled Before Stopping: 25m
- Mass of the block, m=2kg
- Initial velocity, u=10m/s
- Coefficient of friction, μ=0.2
The normal force N acting on the block is equal to the weight of the block since it is on a horizontal surface.
N=mg
Where g (acceleration due to gravity) is approximately 10m/s2.
N=2kg×10m/s2=20N
The frictional force f can be calculated using the formula:
f=μN
Substituting the values:
f=0.2×20N=4N
Since the block is moving to the right (in the direction of the initial velocity), the frictional force will act in the opposite direction (to the left) to oppose the motion.
Using Newton's second law, the retardation a can be calculated as:
a=fm
Substituting the values:
a=4N2kg=2m/s2
Using the equation of motion:
v=u−at
Where v (final velocity) is 0 when the block stops. Rearranging gives:
0=10m/s−(2m/s2)t
Solving for t:
t=10m/s2m/s2=5s
Using another equation of motion:
s=ut−12at2
Substituting the known values:
s=(10m/s)(5s)−12(2m/s2)(5s)2
Calculating:
s=50m−12×2×25=50m−25m=25m
- Magnitude of Friction Force: 4N
- Direction of Friction Force: Left (opposite to the direction of motion)
- Time to Stop: 5s
- Distance Traveled Before Stopping: 25m
Topper's Solved these Questions
Similar Questions
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass 1 kg start moving at t = 0 with speed 2m/s on rough horizontal surface with coefficient of friction 0.2. A horizontal force F is applied in the direction of velocity which varies with time as shown in figure. Find the speed (in m/s) of particle at t = 3 s.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is given a velocity u on a rough horizontal surface of friction coefficient μ. The average power imparted by friction until it stops is
AzeroB12μmguCμmguD2μmgu - Question 2 - Select One
A block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
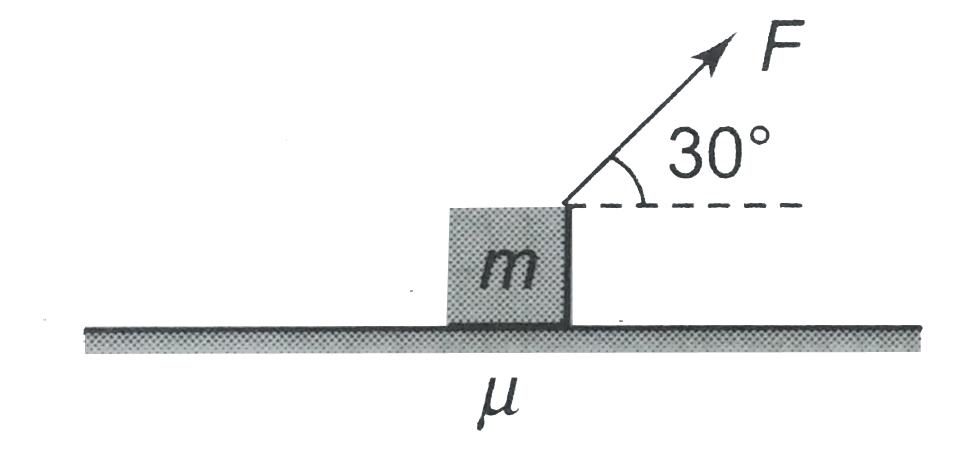 AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2)
AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2) - Question 3 - Select One
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
A0.5m/s2B5m/s2C10m/s2D15m/s2
A block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?
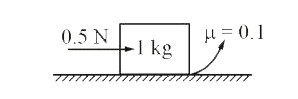 View Solution
View SolutionA block of mass m is given velocity v0 on a rough horizontal surface. After traveling a distance d. Its speed becomes (v0)/(2). Find the work done against friction. The work donw by friction and the coefficient of friction.
View SolutionA block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block
 View Solution
View SolutionA body of mass 10 kg is pulled with a time varying horizontal force F=2t2 N on a rough surface having friction coefficient μ=0.2. Find the speed of block after 6 seconds.
View SolutionA block of mass 5kg is initially at rest on a rough horizontal surface. A force of 45N acts over a distance of 2m. The force of friction acting on the block is 25N. The final kinetic energy of the block is
View Solution

