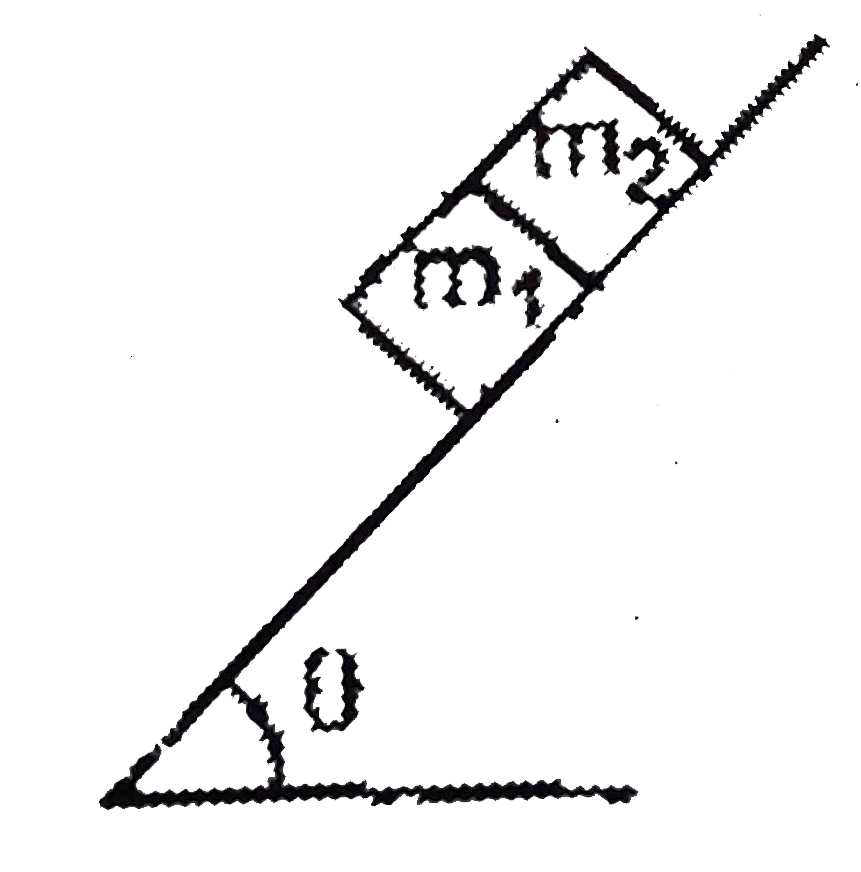
Two blocks are in contect moving on an inclined plane of inclination $α$ with the horizontal. The masses of the blocks are equal to $m_{1}$ and $m_{2}$ and the coefficients of friction between the inclined plane and the blocks are equal to $μ_{1}$ and $μ_{2} (μ_{1} > μ_{2})$ respectively. Find (a) common acceleration of the blocks and (b) the contact force between the blocks.

Video Solution

Text Solution

Verified by Experts

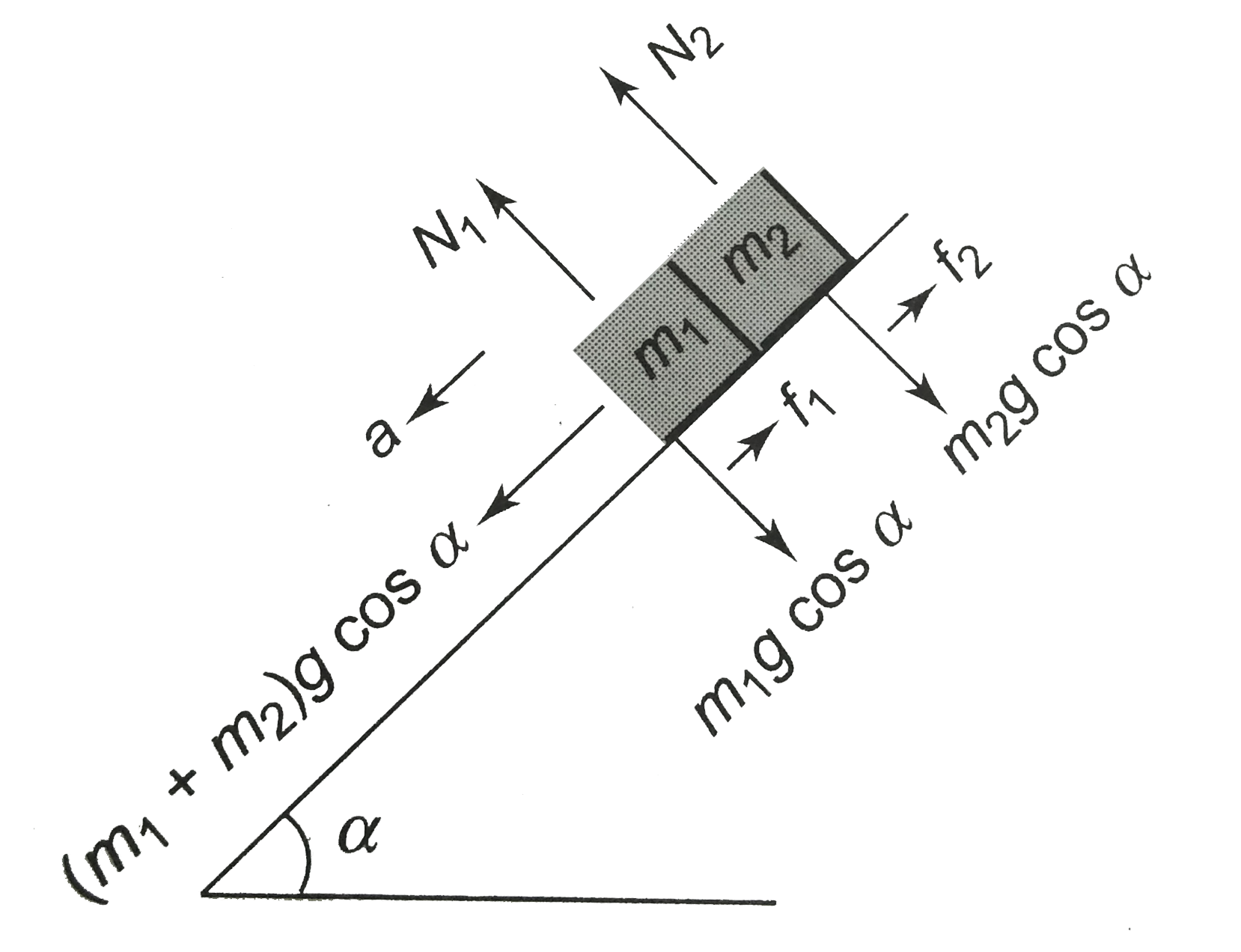
(a) $N_{1} = m_{1} g cos α, f_{1} = μ_{1} N_{1} = m_{1} g cos α$
$N_{2} = m_{2} g cos α, f_{2} = μ_{2} N_{2} = μ_{2} m_{2} g cos α$
Along the plane :
$(m_{1} + m_{2}) g sin α - (f_{1} + f_{2}) = (m_{1} + m_{2}) a$
$a = \frac{(m_{1} + m_{2}) g sin α - (μ_{1} m_{1} + μ_{2} m_{2}) g cos α}{(m_{1} + m_{2})}$
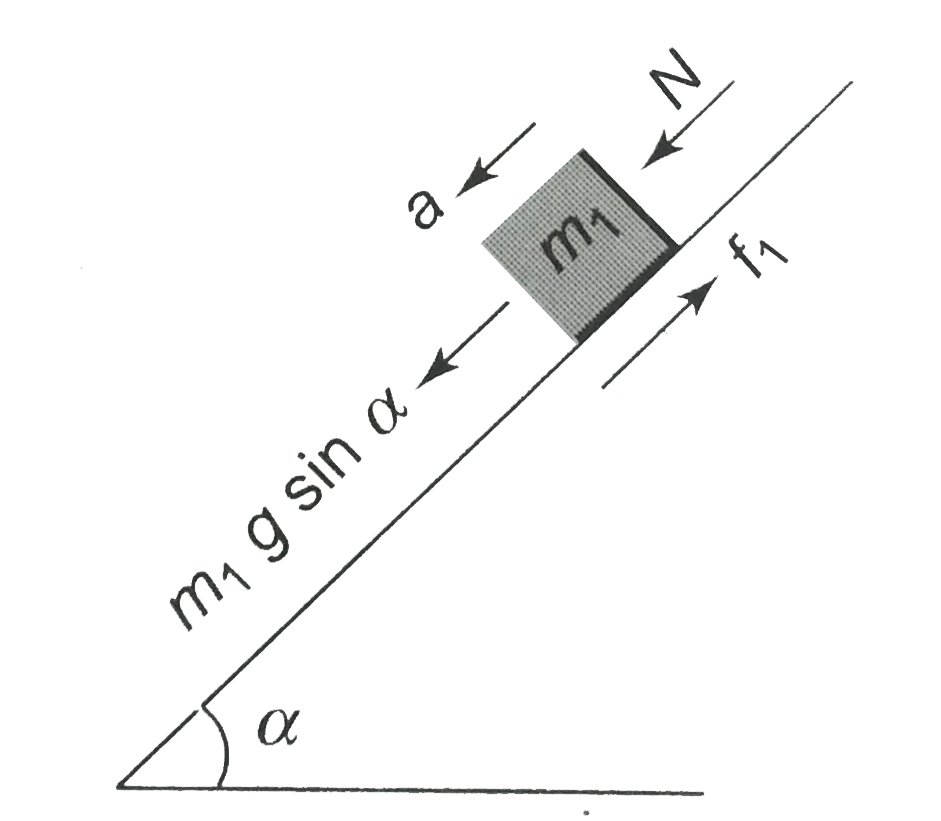
(b) Consider motion of $m_{1}$ : (let the contact force between the blocks in $N$ )
$m_{1} g sin α + N - f_{1} = m_{1} a$
$m_{1} g sin α + N - μ_{1} m_{1} g cos α = m_{1} a$
$N = m_{1} g sin α - \frac{(μ_{1} m_{1} + μ_{2} m_{2}) g cos α m_{1}}{(m_{1} + m_{2})}$
$= μ_{1} m_{1} g cos α - \frac{m_{1} g cos α (μ_{1} m_{1} + μ_{2} m_{2})}{(m_{1} + m_{2})}$
$= m_{1} g cos α [\frac{μ_{1} (m_{1} + m_{2}) - (μ_{1} m_{1} + μ_{2} m_{2})}{(m_{1} + m_{2})}]$
$= \frac{(μ_{1} - μ_{2}) m_{1} m_{1} g cos α}{(m_{1} + m_{2})}$
Since $μ_{1} > μ_{2}$ , direction $N$ is correct.

Updated on:21/07/2023

A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is $μ$ then
.
A $μ > tan θ$
B $f = m g sin θ$
C $f = μ m g cos θ$
Dthe reaction of the ground on the block is mg cos $θ$
A block of mass $m$ is placed at rest on an inclination $θ$ to the horizontal.If the coefficient of friction between the block and the plane is $μ$ , then the total force the inclined plane exerts on the block is
A $m g$
B $μ m g cos θ$
C $m g sin θ$
D $μ m g tan θ$
A block of mass m slides down an inclined plane of inclination $θ$ with uniform speed. The coefficient of friction between the block and the plane is $μ$ . The contact force between the block and the plane is
Amg
B $m g sin θ \sqrt{1 + μ^{2}}$
C $m g sin θ$
D $\sqrt{{(m g sin θ)}^{2} + {(μ m g cos θ)}^{2}}$