A block is placed on an inclined plane whose angle of inclination is greater than the angle of repose. If the coefficient of friction is $μ$ (a) find force $P$ applied parallel to incline that will keep it in equilibrium (minimum and maximum value of force). (b) Find the range of $P$ if it is applied horizontally on the block. ( c) What is the minimum value of $P$ if it is applied perpendicular to the inclined plane?

Text Solution

Verified by Experts

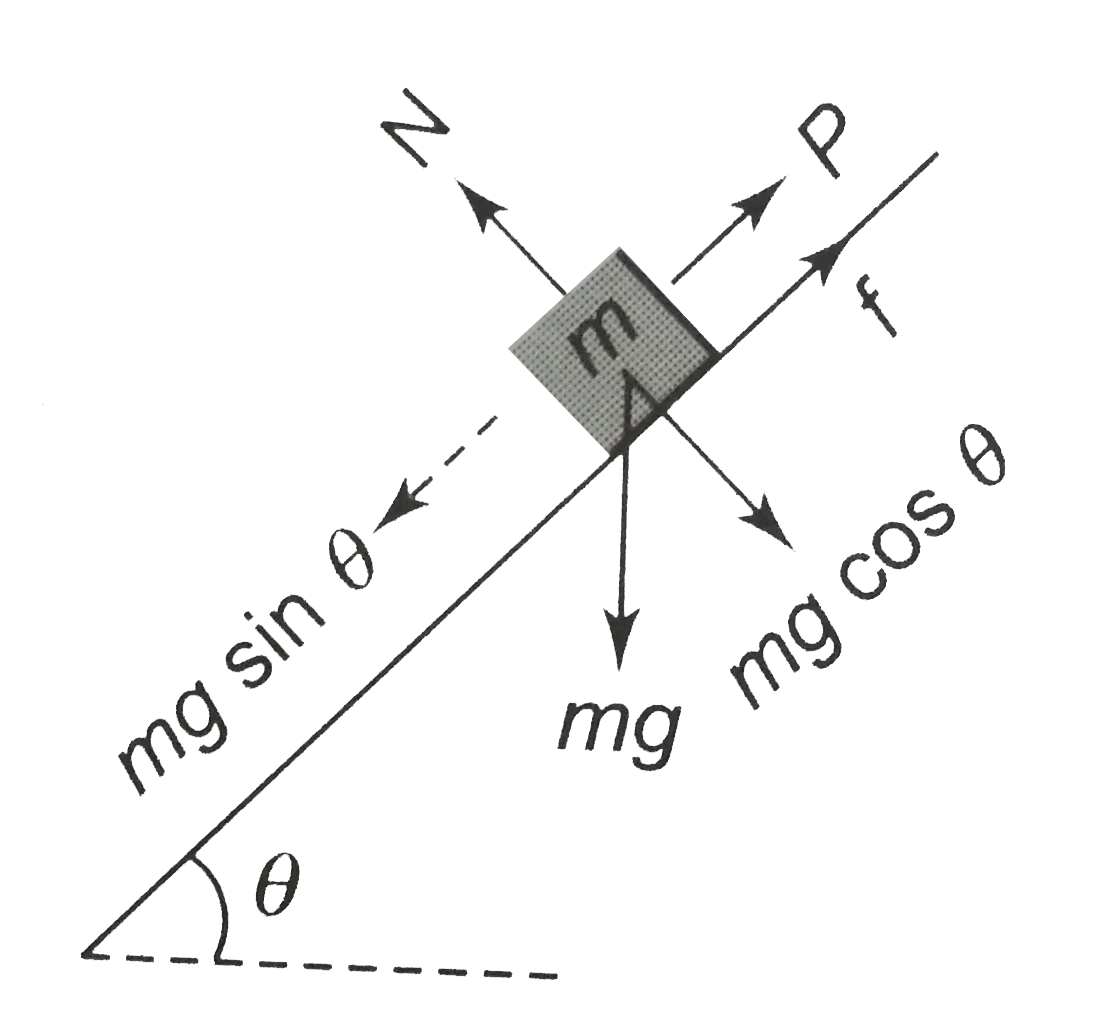
(a)
(i) If the block has tendency to move down , friction will act in the upward direction
$⊥^{a r}$ to the plane : $N = m g cos θ, f = μ N = μ m g cos θ$
Along the plane : $P + f = m g sin θ \to P = m g sin θ - f$
$P_{min} = m g sin θ - μ m g cos θ$
$= m g (sin θ - μ cos θ)$
(ii) If the block has tendency to move up , friction will act in the downward direction
$P = m g sin θ + f$
$P_{max} = m g (sin θ + μ cos θ)$
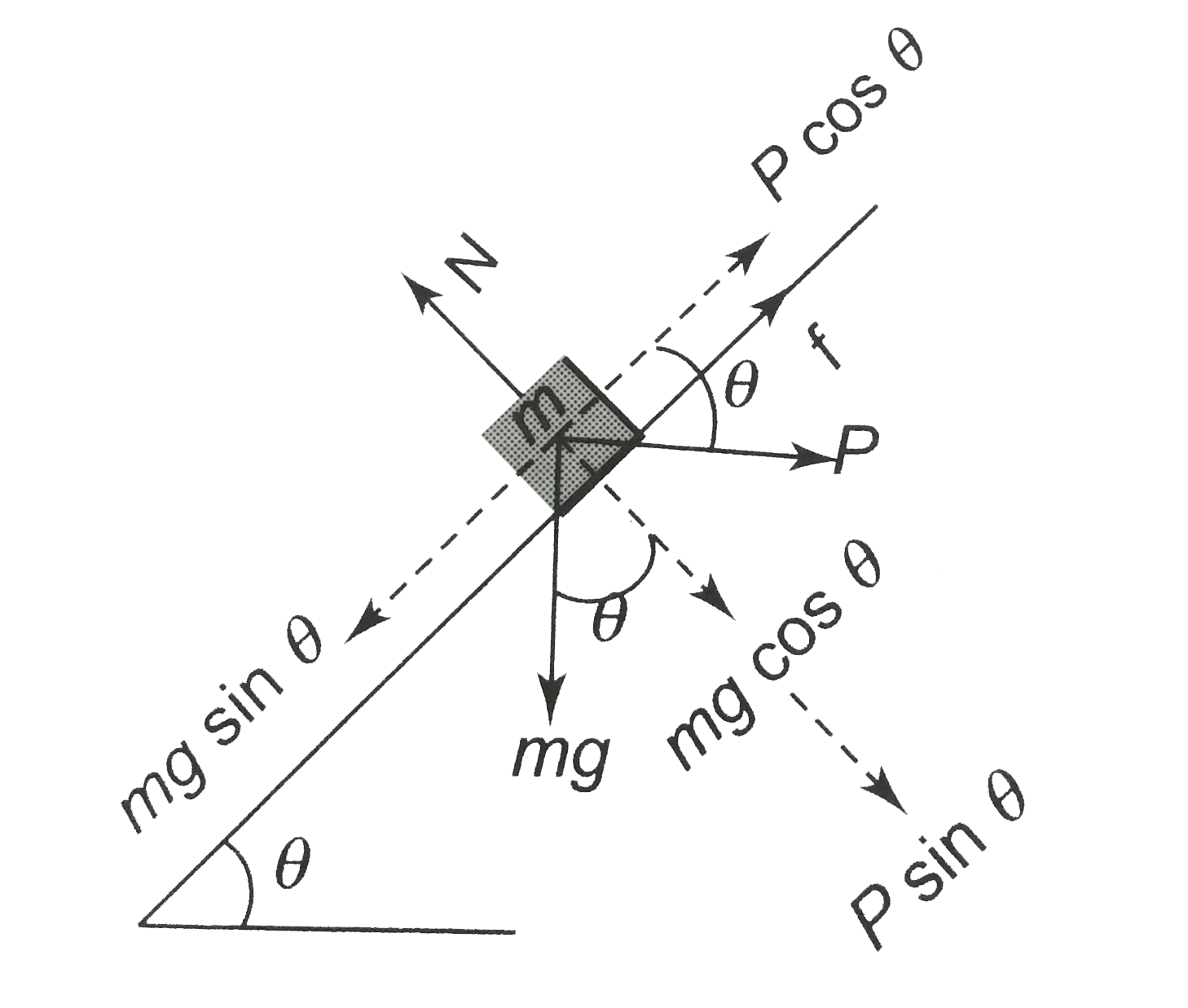
(b) (i) If the block has tendency to move down , friction will act in the upward direction
$⊥^{a r}$ to the plane : $N = m g cos θ + P sin θ$
$f = μ N = μ (m g cos θ + P sin θ)$
Along the plane : $P cos θ + f = m g sin θ$
$P cos θ + μ (P sin θ + m g cos θ) = m g sin θ$
$P (cos θ + μ sin θ) = m g (sin θ - μ cos θ)$
$P = \frac{m g (sin θ - μ cos θ)}{(cos θ + μ sin θ)}$
$P_{min} = \frac{m g (tan θ - μ)}{(1 + μ tan θ)}$
(ii) If the block has tendency to move up , friction will act downwards
$P_{max} = \frac{m g (tan θ + μ)}{(1 - μ tan θ)}$
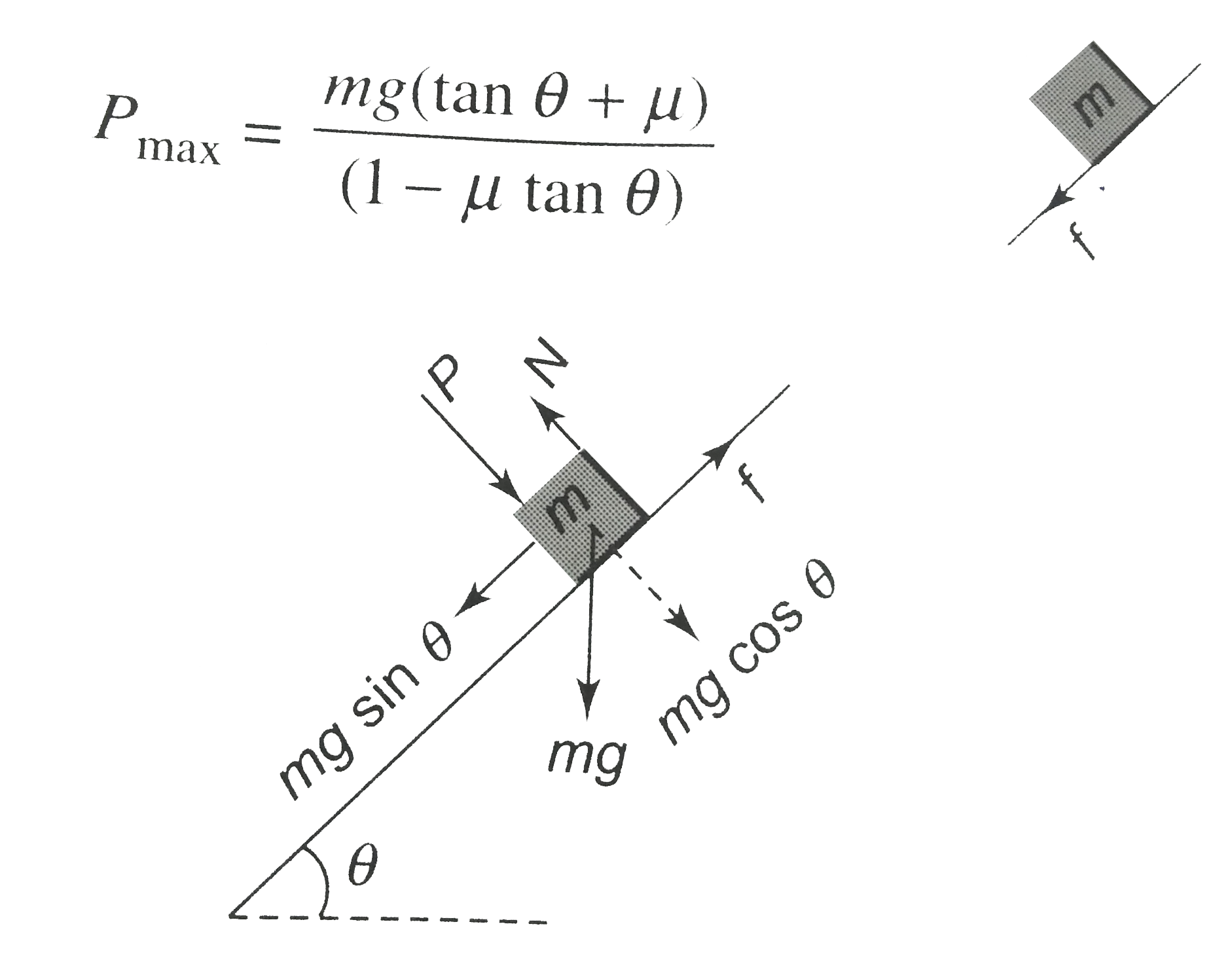
( c) $⊥^{a r}$ to the plane : $N = P + m g cos θ, f = μ N = μ (P + m g cos θ)$
Along the plane : $m g sin θ = f = μ (P + m g cos θ)$
$P_{min} = m g (\frac{sin θ}{μ} - cos θ)$

Updated on:21/07/2023

A block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
A $sin θ$
B $cos θ$
C $cot θ$
D $tan θ$
A block of mass $m$ is placed at rest on an inclination $θ$ to the horizontal.If the coefficient of friction between the block and the plane is $μ$ , then the total force the inclined plane exerts on the block is
A $m g$
B $μ m g cos θ$
C $m g sin θ$
D $μ m g tan θ$