Find the acceleration and tension in the string in the following cases . The pulley and string are massless.
(a)
(b)

Text Solution

Verified by Experts

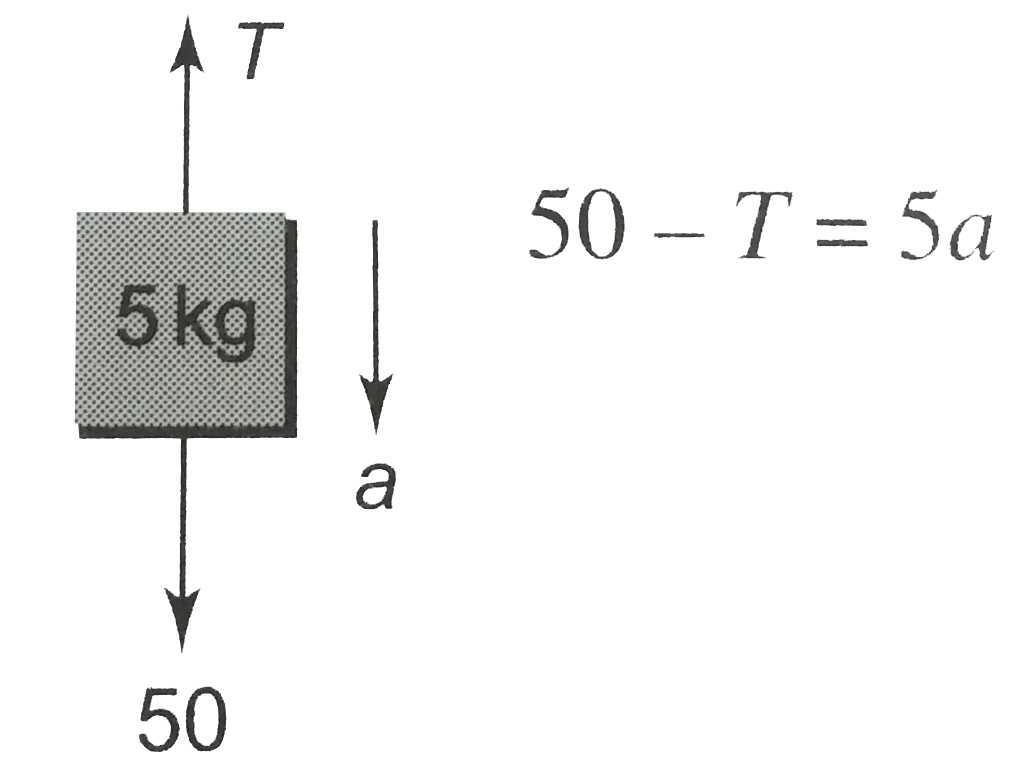
(a) $50 - T = 5 a$ (i)
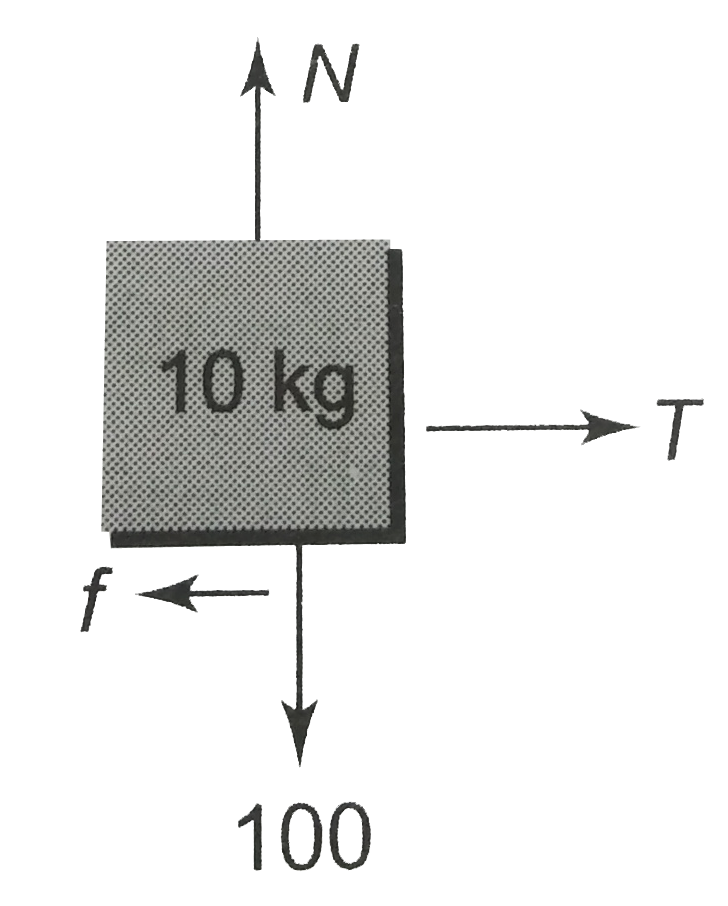
$↑ : N - 100 = 0 \Rightarrow N = 100$
$f = μ N = 0.6 \times 100 = 60 N$
$T - f = 10 a$
$T - 60 = 10 a$ (ii)
Solving $a = - \frac{2}{3} m / s^{2}$ , but the acceleration cannot be negative . The blocks are at rest, $T = 50 N$ .
In this problem , we committed a mistake , we applied the maximum value of friction force but friction is a self - adjusting force which varies from zero to a certain maximum value. Here the value of friction $50 N$ is sufficient to prevent relative motion. When there is relative motion , friction is fully developed but when the blocks are at rest , friction or acceleration force $= 5 g = 50 N$ , opposing force (maximum value) $= 60 N$ .
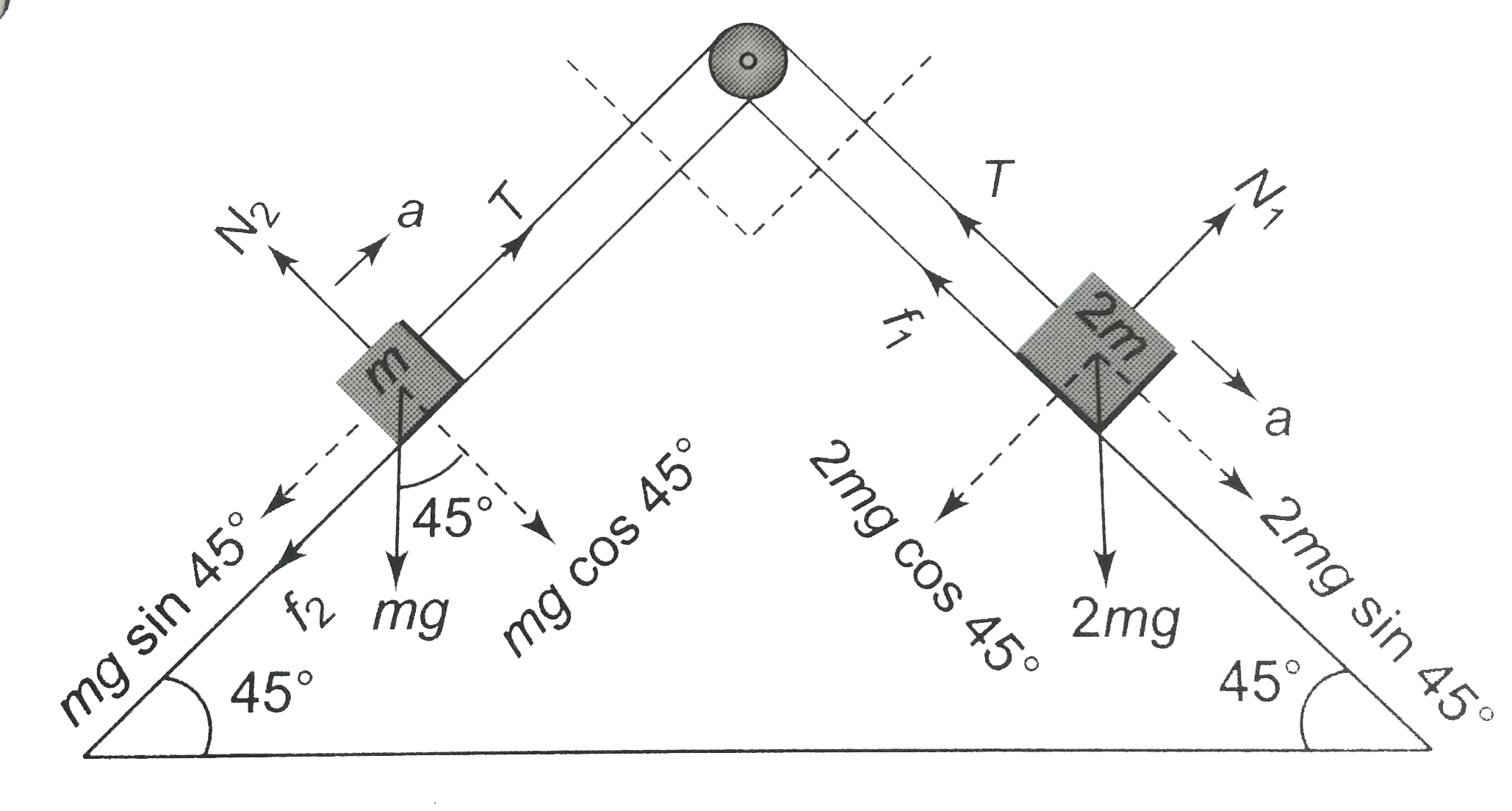
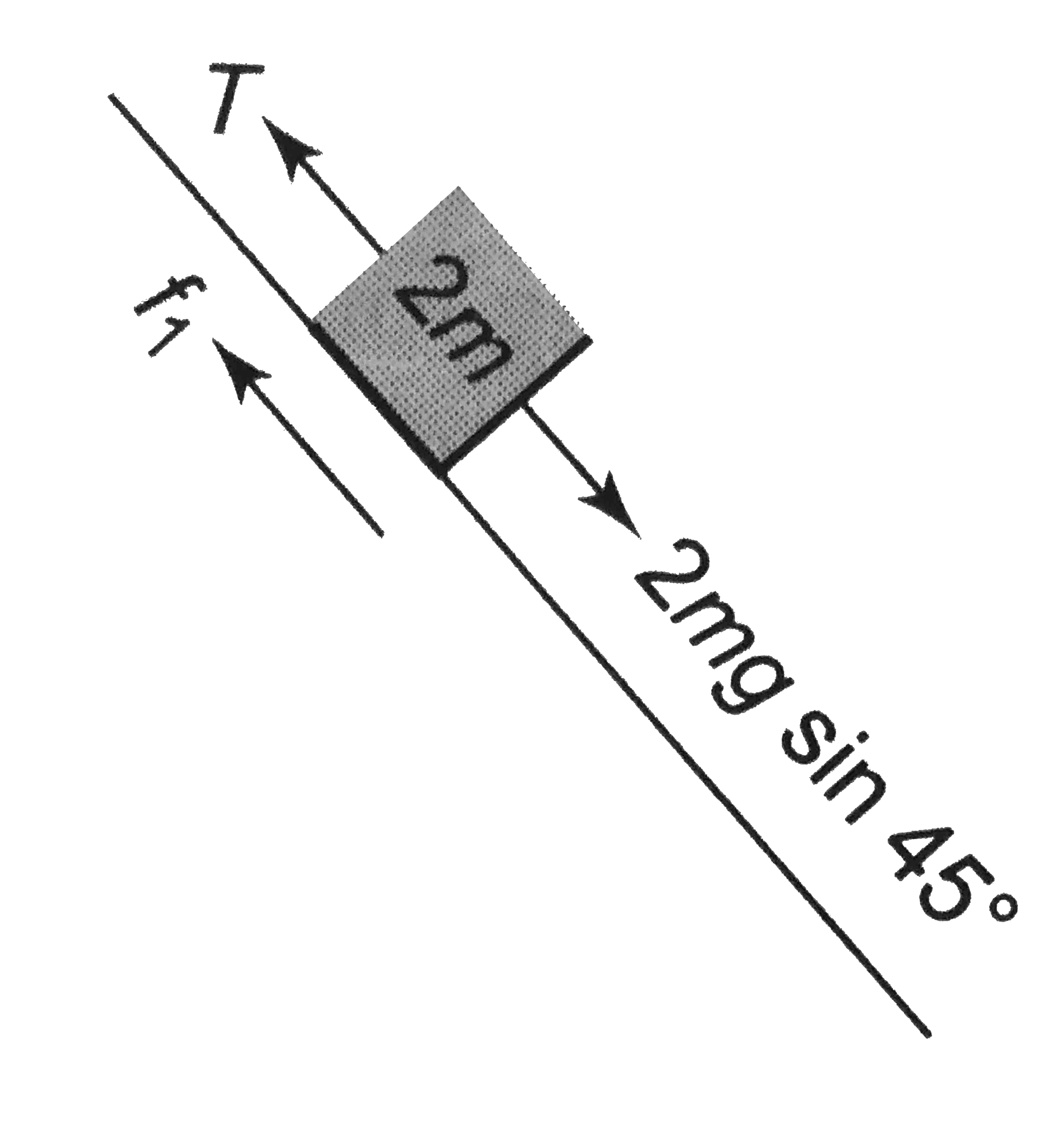
(b) For block of mass $2 m$ ,
$N_{1} = 2 m g {cos 45}^{\circ} = \sqrt{2} m g$
$f_{1} = μ_{1} N_{1} = \frac{\sqrt{2}}{3} m g$
Along the plane : $2 m g {sin 45}^{\circ} - T - F_{1} = 2 m a$
$\sqrt{2} m g - T - \frac{\sqrt{2}}{3} m g = 2 m a$ (i)
For block of mass $m$ :
$N_{2} = m g {cos 45}^{\circ} = \frac{m g}{\sqrt{2}}$ .
$f_{2} = μ_{2} N_{2} = \frac{2 m g}{3 \sqrt{2}}$
Along the plane : $T - m g {sin 45}^{\circ} - f_{2} = m a$
$T - \frac{m g}{\sqrt{2}} - \frac{2 m g}{3 \sqrt{2}} = m a$ (ii)
Adding (i) and (ii) , we get
$3 m a = - \frac{2 m g}{3 \sqrt{2}} \Rightarrow a = - \frac{g}{9 \sqrt{2}} = - v e$
Let the block of mass $m$ move downward by solving , acceleration comes out to be $- v e$ , i.e. system will not move , the blocks are at rest.
OR
Let the block of mass $2 m$ moves downward , the force which tries to accelerate the system $= 2 m g {sin 45}^{\circ} - m g {sin 45}^{\circ} = \frac{m g}{\sqrt{2}}$ .
Oppsing force $= f_{1} + f_{2} = (\frac{\sqrt{2}}{3} + \frac{2}{3 \sqrt{2}}) m g = \frac{4 m g}{3 \sqrt{2}}$
$\frac{m g}{\sqrt{2}} < \frac{4 m g}{3 \sqrt{2}}$ , so the system is at rest
Tension : Block of mass $2 m$
$2 m g {sin 45}^{\circ} = T + f_{1}$
$\sqrt{2} m g = T + \frac{\sqrt{2}}{3} m g$
$T = (\sqrt{2} - \frac{\sqrt{2}}{3}) m g = \frac{2 \sqrt{2} m g}{3}$
Block of mass $m$
$T = m g {sin 45}^{\circ} + f_{2} = \frac{m g}{\sqrt{2}} + f_{2}$
$f_{2} = (\frac{2 \sqrt{2}}{3} - \frac{1}{\sqrt{2}}) = \frac{m g}{3 \sqrt{2}}$
The friction force is fully developed , where the friction coefficient is smaller , hence we have to use the block of $2 m$ to find tension.

Updated on:21/07/2023

|

Class 11 PHYSICS FRICTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

The tension in the string in the pulley system shown in
.
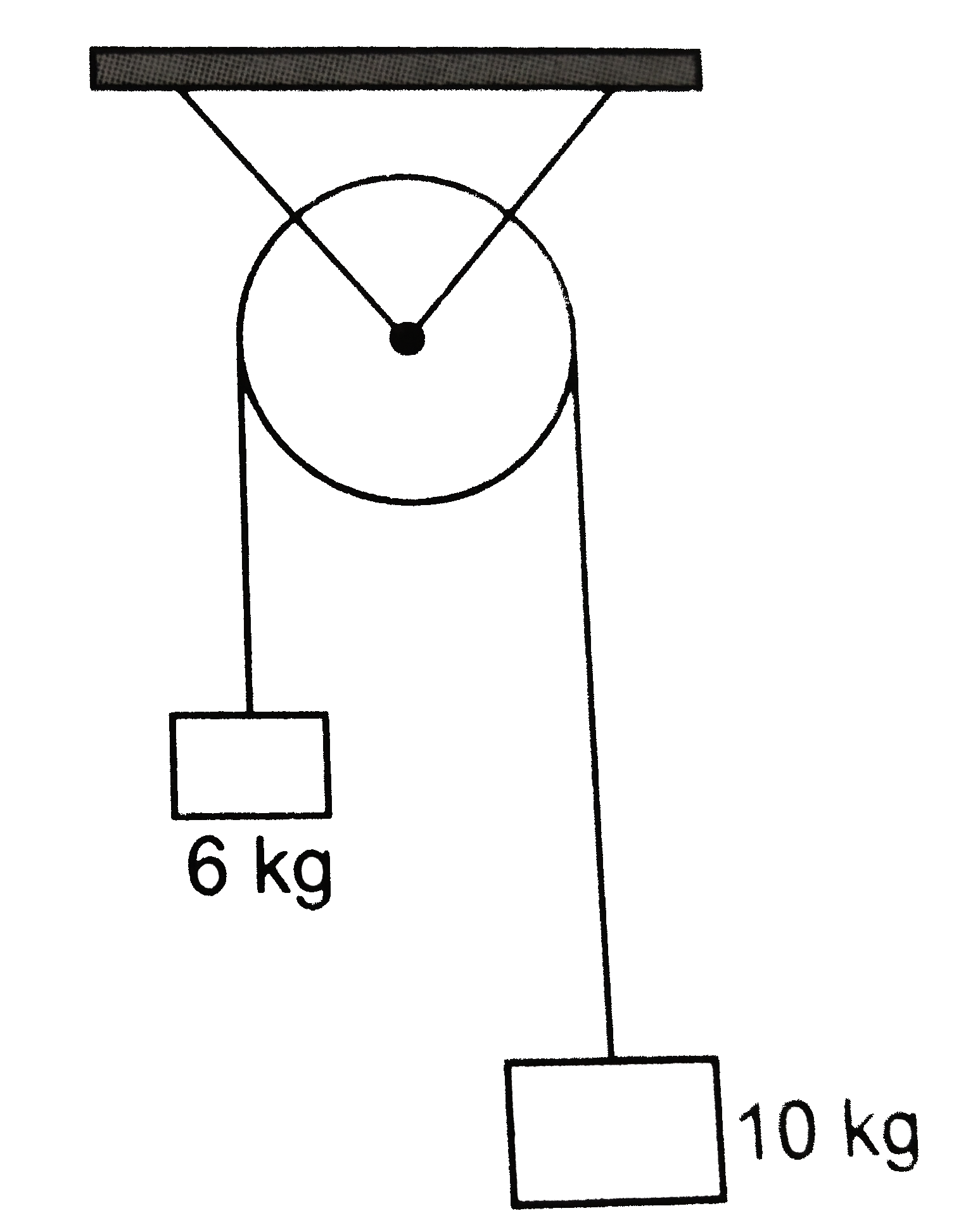A $5.7 N$
B $7 N$
C $7.5 N$
D $73.5 N$

CP SINGH-FRICTION-Exercises

Home
Ask Doubt
Profile