A cubical block of mass is sliding on an inclined right angle trough as shown in the figure. If coefficient of friction is , find the acceleration of the block.
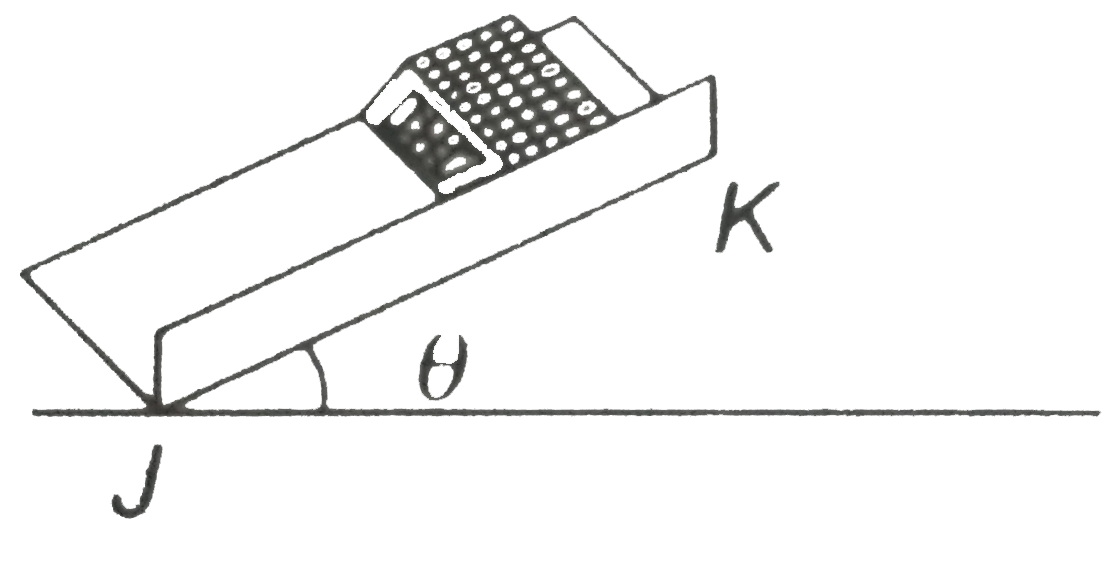
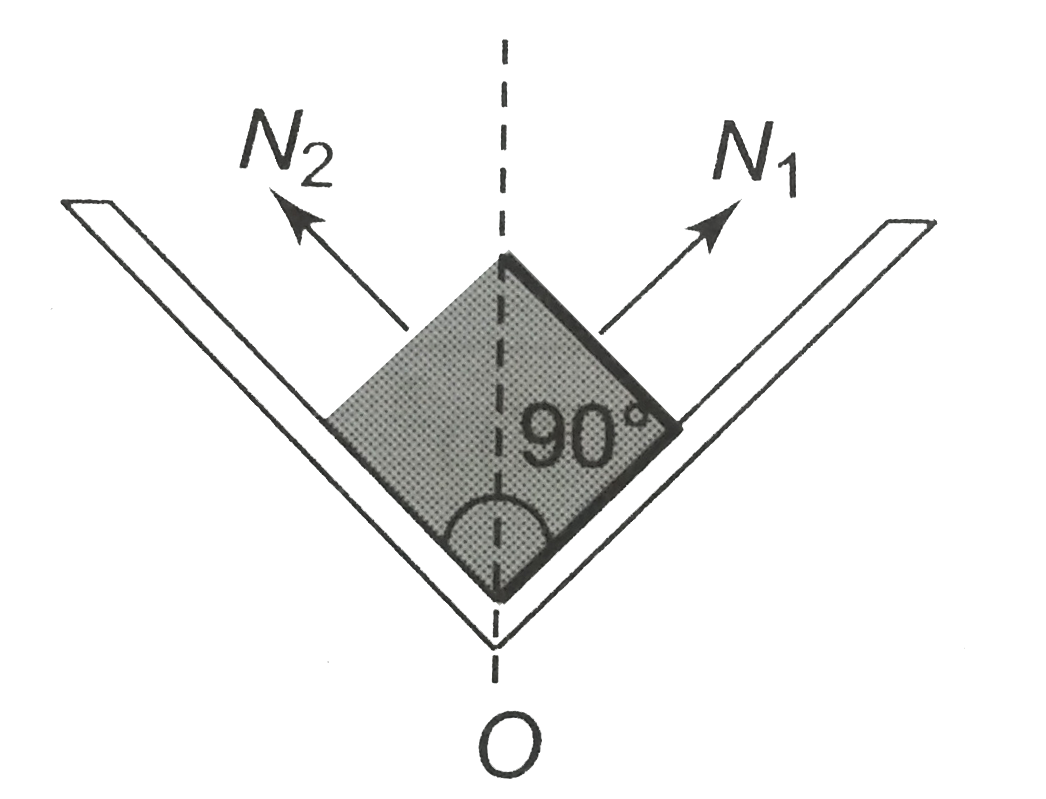
For the cubical block ,
Resultant reaction
Along the plane :

Topper's Solved these Questions
Similar Questions
A block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is

View Solution
Knowledge Check
A block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is
 Ag(sinθ+√2μkcosθ)Bg(sinθ+μkcosθ)Cg(sinθ−√2μkcosθ)Dg(sinθ−μkcosθ)
Ag(sinθ+√2μkcosθ)Bg(sinθ+μkcosθ)Cg(sinθ−√2μkcosθ)Dg(sinθ−μkcosθ)A cubical block of mass √2kg is sliding down on a smooth inclined right angled trough as shown in the figure. The two adjacent surface of cube are always in contact with the trough. Then the net reaction force on the block is
 A10NB2NC√2ND1N
A10NB2NC√2ND1NA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isAμgBμMmgCμmMgDgμ
A block of mass m slides in right angled incliine through as shown in the figure . If the coefficient of kinetic friction between the block and the through is μk , find the acceleration of the block .

View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
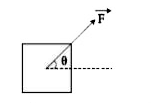
View SolutionA block of mass m slides along a floor while a force of magnitude F is applied to it at an angle θ as shown in figure. The coefficient of kinetic friction is μr. Then, the block's acceleration 'a' is given by:
(g is acceleration due to gravity)
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View Solution
