A steel bar of cross sectional area 1cm2 and 50cm long at 300C fits into the space between two fixed supports.. If the bar s now heated to 2800C, what force will it exert against the supports ? (⋅ for steel =11×106/0C and Young's modulus for steel =2×1011N/m2)
To solve the problem of the steel bar exerting force against the supports when heated, we will follow these steps:
1. Identify the Given Values:
- Cross-sectional area A=1cm2=1×10−4m2
- Original length L=50cm=0.5m
- Initial temperature T1=30∘C
- Final temperature T2=280∘C
- Coefficient of linear expansion for steel α=11×10−6per ∘C
- Young's modulus for steel Y=2×1011N/m2
2. Calculate the Change in Temperature (ΔT):
ΔT=T2−T1=280∘C−30∘C=250∘C
3. Calculate the Change in Length (ΔL):
The formula for change in length due to thermal expansion is:
ΔL=L⋅α⋅ΔT
Substituting the values:
ΔL=0.5m⋅(11×10−6per ∘C)⋅(250∘C)
ΔL=0.5⋅11⋅250×10−6=0.5⋅2750×10−6=1.375×10−3m
4. Calculate the Strain (ϵ):
Strain is defined as:
ϵ=ΔLL
Substituting the values:
ϵ=1.375×10−3m0.5m=0.00275
5. Calculate the Stress (σ):
Stress can be calculated using Young's modulus:
σ=Y⋅ϵ
Substituting the values:
σ=(2×1011N/m2)⋅0.00275=5.5×108N/m2
6. Calculate the Force (F):
The force exerted by the bar against the supports is given by:
F=σ⋅A
Substituting the values:
F=(5.5×108N/m2)⋅(1×10−4m2)=5.5×104N
F=55,000N=55kN
Final Answer:
The force exerted by the steel bar against the supports when heated to 280∘C is 55 kN.
- Cross-sectional area A=1cm2=1×10−4m2
- Original length L=50cm=0.5m
- Initial temperature T1=30∘C
- Final temperature T2=280∘C
- Coefficient of linear expansion for steel α=11×10−6per ∘C
- Young's modulus for steel Y=2×1011N/m2
ΔT=T2−T1=280∘C−30∘C=250∘C
The formula for change in length due to thermal expansion is:
ΔL=L⋅α⋅ΔT
Substituting the values:
ΔL=0.5m⋅(11×10−6per ∘C)⋅(250∘C)
ΔL=0.5⋅11⋅250×10−6=0.5⋅2750×10−6=1.375×10−3m
Strain is defined as:
ϵ=ΔLL
Substituting the values:
ϵ=1.375×10−3m0.5m=0.00275
Stress can be calculated using Young's modulus:
σ=Y⋅ϵ
Substituting the values:
σ=(2×1011N/m2)⋅0.00275=5.5×108N/m2
The force exerted by the bar against the supports is given by:
F=σ⋅A
Substituting the values:
F=(5.5×108N/m2)⋅(1×10−4m2)=5.5×104N
F=55,000N=55kN
The force exerted by the steel bar against the supports when heated to 280∘C is 55 kN.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL-III
Explore 22 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL-I (C.W.)
Explore 23 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL-I(H.W.)
Explore 21 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Exercise
Explore 187 Videos
Similar Questions
A stell wire of cross-sectional area 0.5mm2 is held between teo fixed supports. If the wire is just taut at 20C, determine the tension when the temperature falls to 0C. Coefficient of linear expansion of steel is 1.2×10−50C(−1) and its Young's modulus is 2.0 xx 10^11 N m^(-2).
View SolutionA steel wire of uniform cross-sectional area 2mm2 is heated upto 50∘ and clamped rigidly at two ends . If the temperature of wire falls to 30∘ then change in tension in the wire will be , if coefficient of linear expansion of steel is 1.1×10−5/∘C and young's modulus of elasticity of steel is 2×1011N/m2
View Solution
Knowledge Check
A steel wire 2 mm in diameter is just stretched between two fixed points at a temperature of 20∘C. If the temperature falls to 10∘C, then the tension in the wire is (The coefficient of linear expansion of steel = 11×10−6/∘C and Y for steel 2.1×1011N/m2)
A7.25 NB725 NC72.5 ND7.25×103NA steel wire of length 20 cm and uniform cross-section 1mm2 is tied rigidly at both the ends. If the temperature of the wire is altered from 40∘C to 20∘C, the change in tension. [Given coefficient of linear expansion of steel is 1.1×105.∘C−1 and Young's modulus for steel is 2.0×1011Nm−2]
A22 NB44 NC66 ND88 N
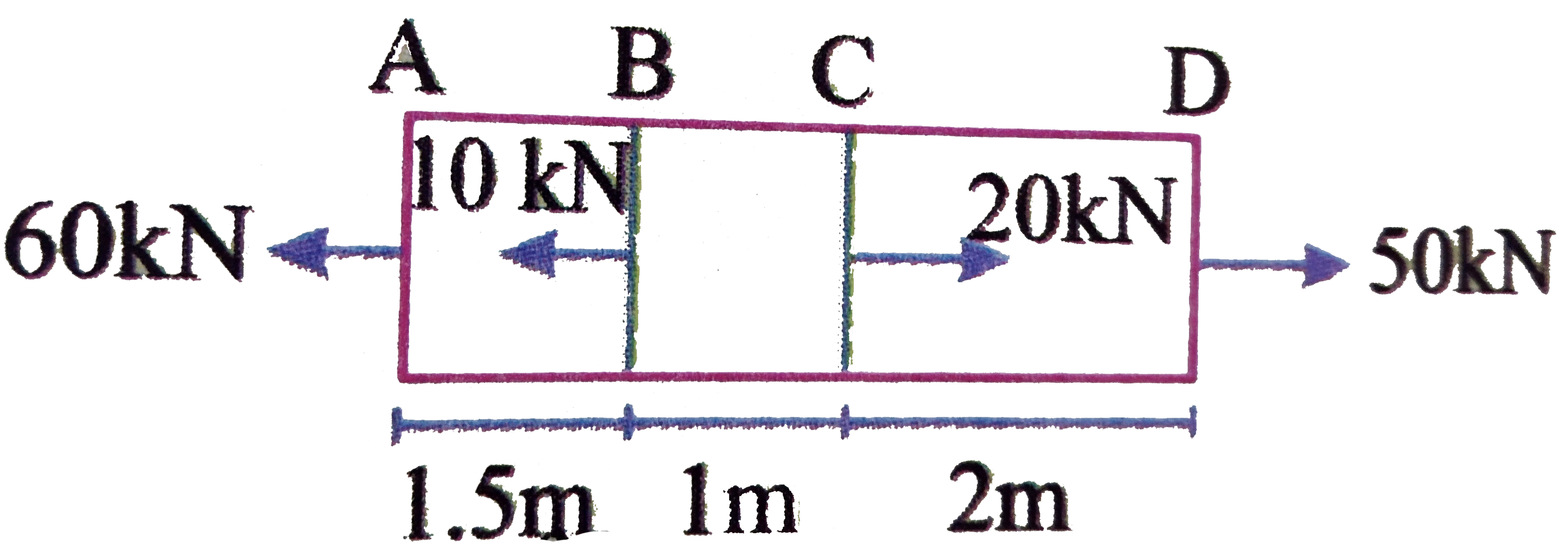
A steel rod of cross-sectional area 1m2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
View SolutionA steel wire 2mm in diameteris ust streched between two dixed point at a temperature of 20∘C. Determine its tension when its temperature falls to 10∘C. Linear expansivity of steel =11×10−6/K,Youngmodu––s=2 xx 10^(11)//m^(-2)
View SolutionYoung 's modulus of steel is 2.0×1011Nm/(2). Express it is dynecm2.
View SolutionA steel wire of length 20 cm and unifrom crossection mm2 is tied rigidly at both the ends. If temperature of the wre is altered from 40∘C to 20∘C, calcutlate the change in tension. Given coeffeicient of linear expansion of steel is 1.1×10−5.∘C−1 and Young's modulus for steel is 2.0×1011Nm−2.
View SolutionA uniform iron wire of cross-section area 0.20 × 10−6 m2 is held fixed in between fixed supports. If wire cooled from 100°C to O°C, then force of 48 N is exerted on supports by ends, then expansion coefficient of wire Young's modulus of steel =2×1011N/m2
View SolutionFigure shows a steel rod of cross sectional ara 2×10−6m2 is fixed between two vertical walls. Initially at 20∘C there is no force between the ends of the rod and the walls. Find the force which the rod will exert on walls at 100∘C. Given that the coefficient of linear expansion of steel is 1.2×10−5.∘C−1 and Young's modulus is 2×1011N/m2

View Solution