A vessel contains a gas under a pressure of 5×105pa. If 3/5 of the mass of the gas is flown out, What will be the gas pressure if the temperature being maintained constant,
50MPa
2MPa
0.2MPa
0.5MPa
The correct Answer is:C
To solve the problem step by step, we will use the ideal gas law and the relationship between pressure and mass when temperature and volume are constant.
Step 1: Understand the initial conditions
The initial pressure of the gas in the vessel is given as:
P1=5×105Pa
Step 2: Determine the initial mass
Let the initial mass of the gas be m.
Step 3: Calculate the final mass after gas is flown out
Since 35 of the mass of the gas is flown out, the remaining mass m2 can be calculated as:
m2=m−35m=25m
Step 4: Use the relationship between pressure and mass
According to the ideal gas law, if the temperature is constant and the volume of the vessel does not change, the pressure of the gas is directly proportional to its mass. Therefore, we can write:
P2P1=m2m1
Step 5: Substitute the known values
We know:
- P1=5×105Pa
- m2=25m
- m1=m
Substituting these into the equation gives:
P25×105=25mm
This simplifies to:
P25×105=25
Step 6: Solve for P2
Now, we can solve for P2:
P2=5×105×25
P2=2×105Pa
Step 7: Convert to MegaPascal
To convert P2 from Pascal to MegaPascal:
P2=2×105Pa=0.2MPa
Final Answer
The final pressure of the gas in the vessel after 35 of the mass has flown out is:
P2=0.2MPa
---
The initial pressure of the gas in the vessel is given as:
P1=5×105Pa
Let the initial mass of the gas be m.
Since 35 of the mass of the gas is flown out, the remaining mass m2 can be calculated as:
m2=m−35m=25m
According to the ideal gas law, if the temperature is constant and the volume of the vessel does not change, the pressure of the gas is directly proportional to its mass. Therefore, we can write:
P2P1=m2m1
We know:
- P1=5×105Pa
- m2=25m
- m1=m
P25×105=25mm
This simplifies to:
P25×105=25
Now, we can solve for P2:
P2=5×105×25
P2=2×105Pa
To convert P2 from Pascal to MegaPascal:
P2=2×105Pa=0.2MPa
The final pressure of the gas in the vessel after 35 of the mass has flown out is:
P2=0.2MPa
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - V12videos
THERMAL PROPERTIES OF MATTER
- BOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - VI4videos
THERMAL PROPERTIES OF MATTER
- BOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL-I (C.W.)23videos
THERMAL PROPERTIES OF MATTER
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise187videos
THERMODYNAMICS
Similar Questions
A glass container encloses a gas a pressure of 8×105 pa and 300 K temperature. The container walls can bear a maximum pressure of 106 Pa. If the temperature of container is gradually increased, find the temperature at which the container will break.
View SolutionA closed vessel 10L in volume contains a diatomic gas under a pressure of 105N/m2. What amount of heat should be imparted to the gas to increase the pressure in the vessel five times?
View Solution
Knowledge Check
- Question 1 - Select One
A vessel is filled with an ideal gas at a pressure of 10 atmospheres and temp 270C. Half of the mass of the gas is removed from the vessel the temperature of the remaining gas is increased to 870C. Then the pressure of the gas in the vessel will be
A5atmB18atmC7atmD8atm - Question 2 - Select One
Container A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
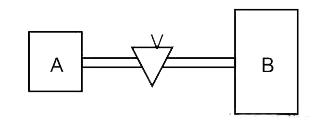
The valve V is adjusted to allow the pressure to equalize, but the temperature of each container is kept constant at the initial value, then the pressure in the two containers is :A4×105 PaB3×105 PaC2×105 PaD1×105 Pa - Question 3 - Select One
A glass container encloses gas at a pressure 4×105 Pa and 300 K temperature. The container walls can bear a maximum pressure of 8×105 Pa. If the temperature of container is gradually increased find temperature at which container will break.
A600KB150KC1200KD375K
A vessel of volume V contains ideal gas at the temperature T0∘C. After a portion of the gas the been let out , the pressure in the vessel decreased by Δp ( the temperature remaining constant). . Find the mass ofthe re.leased gas.The gas density under the noraml conditions ρ
View SolutionOxygen is filled in a closed metal jar of volume 1.0×10−3m3 at a pressure of 1.5×105Pa. and temperature 400K.The jar has a small leak in it. The atmospheric pressure is 1.0×105Pa and the atmospheric temperature is 300K. Find the mass of the gas that leaks out by time the pressure and the temperature inside the jar equlise with the surrounding.
View SolutionA vessel is filled with an ideal gas at a pressure of 20atm and is a temperature of 27∘C One - half of the mass is removed from the vessel and the temperature of the remaining gas is increased to 87∘C. At this temperature, Find the pressure of the gas.
View SolutionA cylinder contains 12kg of gas at presssure of 107 N/m2. The qunatity of gas taken out of the cylinder, if final pressure is 3 Χ 106 N/m2 , will be (temperature of gas is constant)
View SolutionA gas is enclosed in a vessel at a pressure of 2.5atm. Due to leak in the vessel., after some time the pressure is reduced to 2atm, temperature remaining unchanged. The percentage of gas that has leaked out is
View Solution

