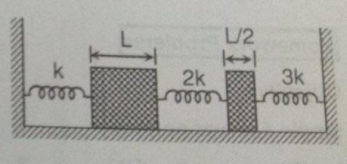
The systeam shown is figure consists of $3$ springs and two rods. If the temperature of the rod is increased by $Δ T$ , then the total energy stored in three springs is $β \times \frac{99}{484} k L^{2} α^{2} {(Δ T)}^{2}$ . Datermine the value of $β$ . The soring are initially relaxed and there is no frication anywhere. For rod the coefficient of linear expansion is $α$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

How much should the temperature of a brass rod be increased so as to increase its length 3% ( $α$ for brass is $2 \times 10^{- 5} /^{\circ} C^{- 1}$ )?
A $1500^{\circ} C$
B $150^{\circ} C$
C $2000^{\circ} C$
D $2500^{\circ} C$
The moment of ineratia of a uniform thin rod about its perpendicular bisector is $I$ . If the temperature of the rod is increased by $Δ t$ , the moment of inertia about perpendicular bisector increases by (coefficient of linear expansion of material of the rod is $α$ ).
AZero
B $I α Δ t$
C $2 I α Δ t$
D $I α Δ t$
When solid is heated , its length changes according to the relation $l = l_{0} (1 + α Δ T)$ , where l is the final length , $l_{0}$ is the initial length , $Δ T$ is the change in temperature , and $α$ is the coefficient of linear is called super - facial expansion. the area changes according to the relation $A = A_{0} (1 + β Δ T)$ , where A is the tinal area , $A_{0}$ is the initial area, and $β$ is the coefficient of areal expansion.
The coefficient of linear expansion of brass and steel are $α_{1} and α_{2}$ If we take a brass rod of length $I_{1}$ and a steel rod of length $I_{2}$ at $0^{\circ} C$ , their difference in length remains the same at any temperature if
A $α_{1} l_{2} = α_{2} l_{2}$
B $α_{1} l_{2}^{2} = α_{2} l_{1}^{2}$
C $α_{1}^{2} l_{2} = α_{2}^{2} l_{1}$
D $α_{1} l_{1} = α_{2} l_{2}$