T1,T2 are time periods of oscillation of a block when individually suspended to springs of force constants K1,K2 respectively. If same block is suspended to parallel combination fo same two springs. Its time period is
T1+T2
T1+T22
T1T2T1+T2
T1T2√T21+T22
The correct Answer is:D
Step by step video, text & image solution for T_(1),T_(2) are time periods of oscillation of a block when individually suspended to springs of force constants K_(1),K_(2) respectively. If same block is suspended to parallel combination fo same two springs. Its time period is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -I (C.W)34videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -II (C.W)36videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV41videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks isView SolutionTwo particles A and B of equal masses are suspended from two massless springs of spring constants K1andK2 respectively. If the maximum velocities during oscillations are equal. the ratio of the amplitude of A and B is
View Solution
Knowledge Check
- Question 1 - Select One
T1,T2 are time periods of oscillation of a block when individually suspended to springs of force constants K1,K2 respectively. If same block is suspended to series combination of same two springs, then it time period of oscillation.
AT1+T2BT1T2T1+T2CT1T2√T21+T22D√T21+T22 - Question 2 - Select One
A mass M is suspended by two springs of force constants K1andK2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is
 AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mg
AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mg - Question 3 - Select One
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
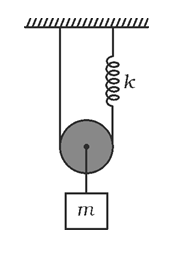 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2k
When a block of mass m is suspended separately by two different springs have time period t1 and t2. If same mass is connected to parallel combination of both springs, then its time period is given by :-
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is
 View Solution
View SolutionLet T1andT2 be the periods of springs A and B when mass M is suspended from one end of each spring. If both springs are taken in series and the same mass A is, suspended from the séries combination, the time period is T, then
View SolutionTwo springs of force constants K1=K2 are stretched by the same force. It W1 and W2 are the energies stored its them respectively, then
View SolutionA mass m performs oscillations of period T when hanged by spring of force constant K . If spring is cut in two parts and arranged in parallel and same mass is oscillated by them, then the new time period will be
 View Solution
View Solution

