A spring of force constant k is cut into two parts whose lengths are in the ratio 1:2. The two parts are now connected in parallel and a block of mass m is suspended at the end of the combined spring. The period of oscillation of block is
2π√2m9K
2π√m9K
2π√2m5K
2π√m5K
The correct Answer is:A
To solve the problem, we need to follow these steps:
Step 1: Understand the Problem
We have a spring with a spring constant k that is cut into two parts in the ratio 1:2. We need to find the period of oscillation when these two parts are connected in parallel and a mass m is suspended from them.
Step 2: Determine the Lengths of the Spring Parts
Let the total length of the spring be L. Since the spring is cut in the ratio 1:2:
- Length of the first part L1=13L
- Length of the second part L2=23L
Step 3: Calculate the Spring Constants of Each Part
The spring constant k is inversely proportional to the length of the spring. Therefore:
- For the first part:
k1=k⋅LL1=k⋅L13L=3k
- For the second part:
k2=k⋅LL2=k⋅L23L=3k2
Step 4: Find the Effective Spring Constant
When springs are connected in parallel, the effective spring constant keffective is the sum of the individual spring constants:
keffective=k1+k2=3k+3k2
To add these, we can find a common denominator:
keffective=3k+1.5k=6k2+3k2=9k2
Step 5: Calculate the Period of Oscillation
The period T of oscillation for a mass m attached to a spring with spring constant keffective is given by the formula:
T=2π√mkeffective
Substituting keffective=9k2:
T=2π√m9k2=2π√2m9k
Final Answer
Thus, the period of oscillation of the block is:
T=2π√2m9k
---
We have a spring with a spring constant k that is cut into two parts in the ratio 1:2. We need to find the period of oscillation when these two parts are connected in parallel and a mass m is suspended from them.
Let the total length of the spring be L. Since the spring is cut in the ratio 1:2:
- Length of the first part L1=13L
- Length of the second part L2=23L
The spring constant k is inversely proportional to the length of the spring. Therefore:
- For the first part:
k1=k⋅LL1=k⋅L13L=3k
- For the second part:
k2=k⋅LL2=k⋅L23L=3k2
When springs are connected in parallel, the effective spring constant keffective is the sum of the individual spring constants:
keffective=k1+k2=3k+3k2
To add these, we can find a common denominator:
keffective=3k+1.5k=6k2+3k2=9k2
The period T of oscillation for a mass m attached to a spring with spring constant keffective is given by the formula:
T=2π√mkeffective
Substituting keffective=9k2:
T=2π√m9k2=2π√2m9k
Thus, the period of oscillation of the block is:
T=2π√2m9k
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL -III
Explore 51 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:NCERT BASED QUESTIONS
Explore 1 Video
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL -I (C.W)
Explore 34 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
Two particles are in SHM in a straight line about same equilibrium position. Amplitude A and time period T of both the particles are equal. At time t=0, one particle is at displacement y1=+A and the other at y2=−A/2, and they are approaching towards each other. after what time they cross each other?
View SolutionThe displacement of a particle is represented by the equation y=3cos(π4−2ωt).
The motion of the particle is
View SolutionThe displacement of a particle in SHM is x=3sin(20πt)+4cos(20πt)cm. Its amplitude of oscillation is
View SolutionA shot putter with a mass of 80kg pushes the iron ball of mass of 6kg from a standing position accelerating it uniformly form rest at an angle of 45∘ with the horizontal during a time interval of 0.1 seconds. The ball leaves his hand when it 2m high above the level ground and hits the ground 2 seconds later (g=10m/s2).
The accleration of the ball in shot putter's hand .
View SolutionWhat is the discovery of CV Raman?
View SolutionTime period of a block with a spring is T_(0) . Now ,the spring is cut in two parts in the ratio 2 : 3 . Now find the time period of same block with the smaller part of the spring.
View SolutionA block of mass M suspended from a spring oscillates with time period T . If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionA spring of force constant k is cut into two equal parts, and mass 'm' is suspended from parallel combination of the springs. Then frequency of small osciollations is
View SolutionA mass m performs oscillations of period T when hanged by spring of force constant K . If spring is cut in two parts and arranged in parallel and same mass is oscillated by them, then the new time period will be

View SolutionThe period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
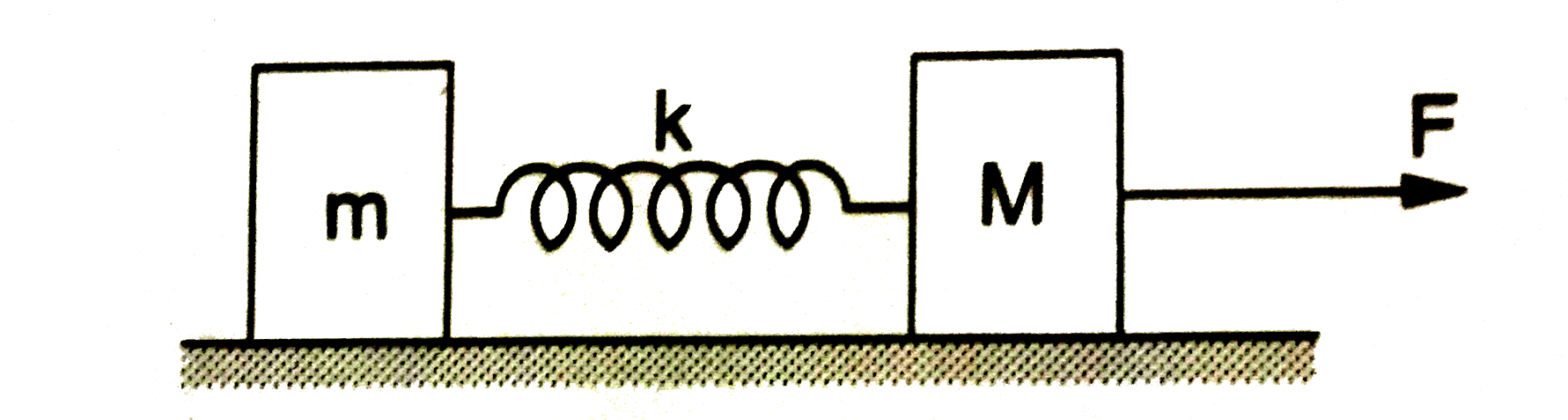
View Solutionचित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके एक घर्षणरहित क्षैतिज सतह पर रखे हैं तथा k स्प्रिंग नियतांक वाले एक स्प्रिंग से जुड़े हैं। प्रारंभ में स्प्रिंग अपनी स्वाभाविक लंबाई में है तथा गुटके स्थिर हैं। अब एक अचर बल F, द्रव्यमान M वाले गुटके पर लगना प्रारंभ करता है। स्प्रिंग की लंबाई में अधिकतम वृद्धि निकालें।
View SolutionA spring having spring constant K is cut into two parts in the ratio 1 : 2 find the spring constants of the two parts .
View SolutionA spring having spring constant k is cut into two parts in the ratio 1:2 Find the spring constants of the two parts.
View SolutionA massless spring, having force constant k, oscillates with a frequency n when a mass m is suspended from it. The spring is cut into two equal halves and a mass 2m is suspended from one of the parts. The frequency of oscillation will now be………….
View SolutionA mass suspended from a spring of spring constant k is made to oscillate with a time period T. Now, the spring is cut into three equal parts and the mass is suspended from one of the parts. What will be the new time period of oscillations?
View Solution