A body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
mgK
mgK√(1+2hKmg)
mgK+mgK√(1+2hKmg)
mgK−mgK√(1+2hKmg)
The correct Answer is:B
F=kx0 and conservation of energy
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - NCERT BASED QUESTIONS1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - MULTIPLE ANSWER QUESTIONS23videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -II (C.W)36videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
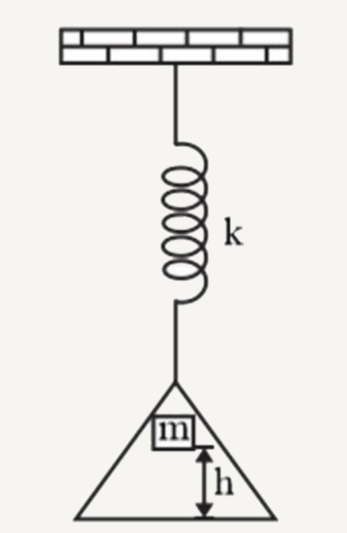 View Solution
View Solution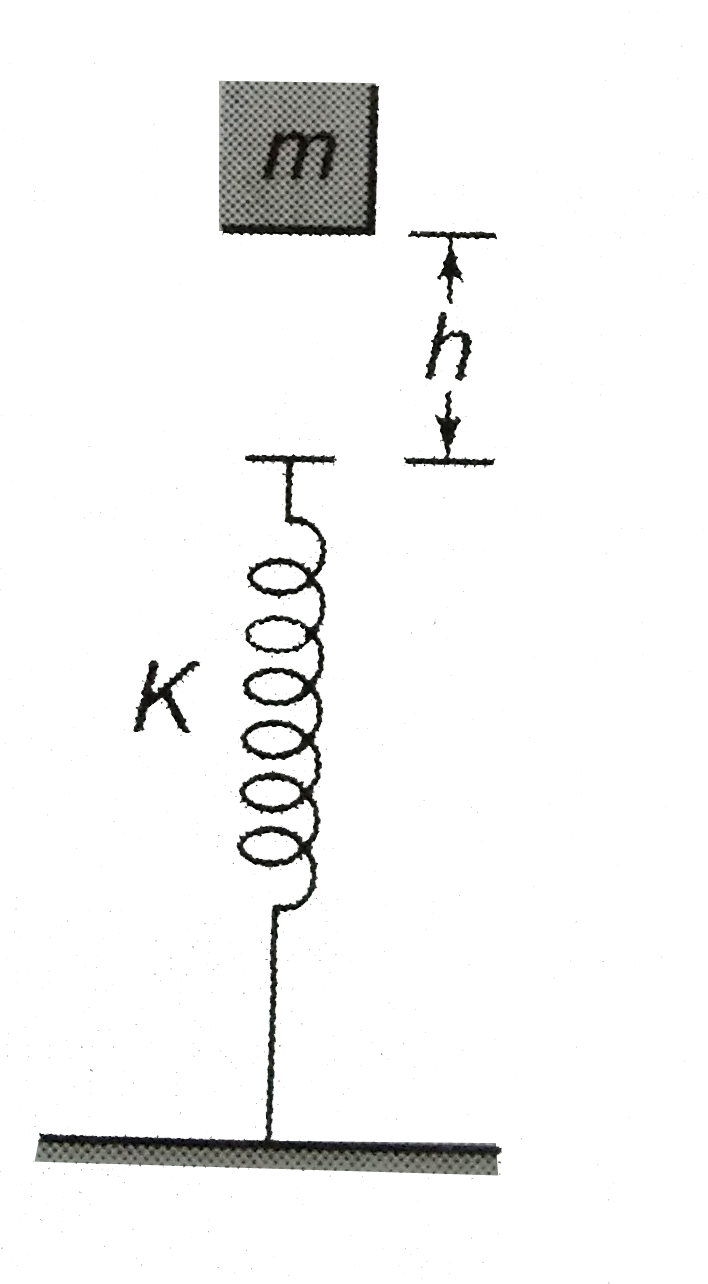
A block is released from height h, find the maximum compression of spring of spring constant k.View Solution
Knowledge Check
- Question 1 - Select One
A body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is
 AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of these
AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of these - Question 2 - Select One
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
 Amg/dBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkMg−mgk)
Amg/dBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkMg−mgk) - Question 3 - Select One
A load of mass m falls from a height h on to the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is
 AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)
AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)
A body of mass m falls from a height h on to the pan of a spring balance. The masses of the pan and spring are negligible. The spring constant of the spring is k. Having stuck to the pan the body starts performing harmonic oscillations in the vertical direction. Find the amplitude and energy of oscillation.
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenView SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is
 View Solution
View SolutionA solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is
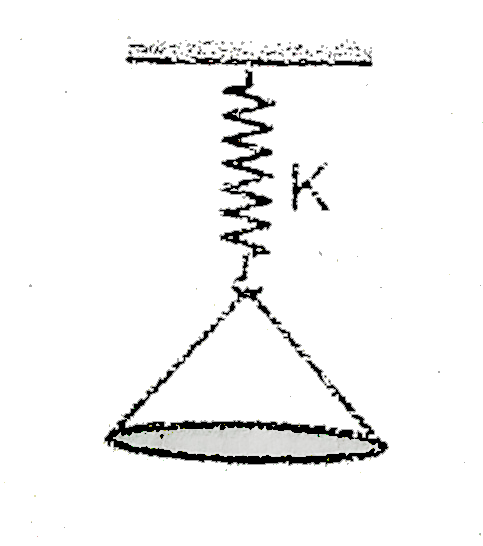 View Solution
View Solution

